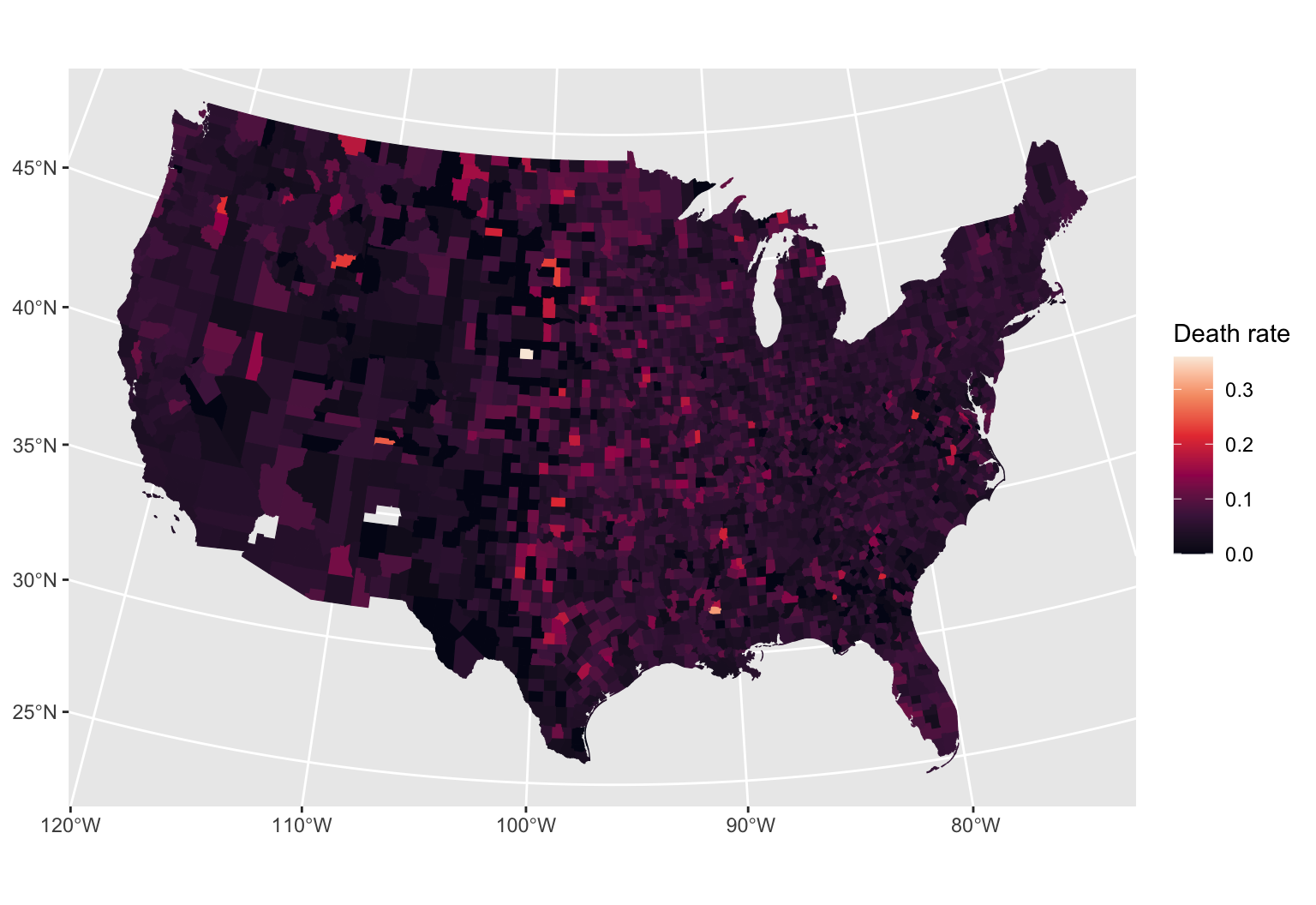
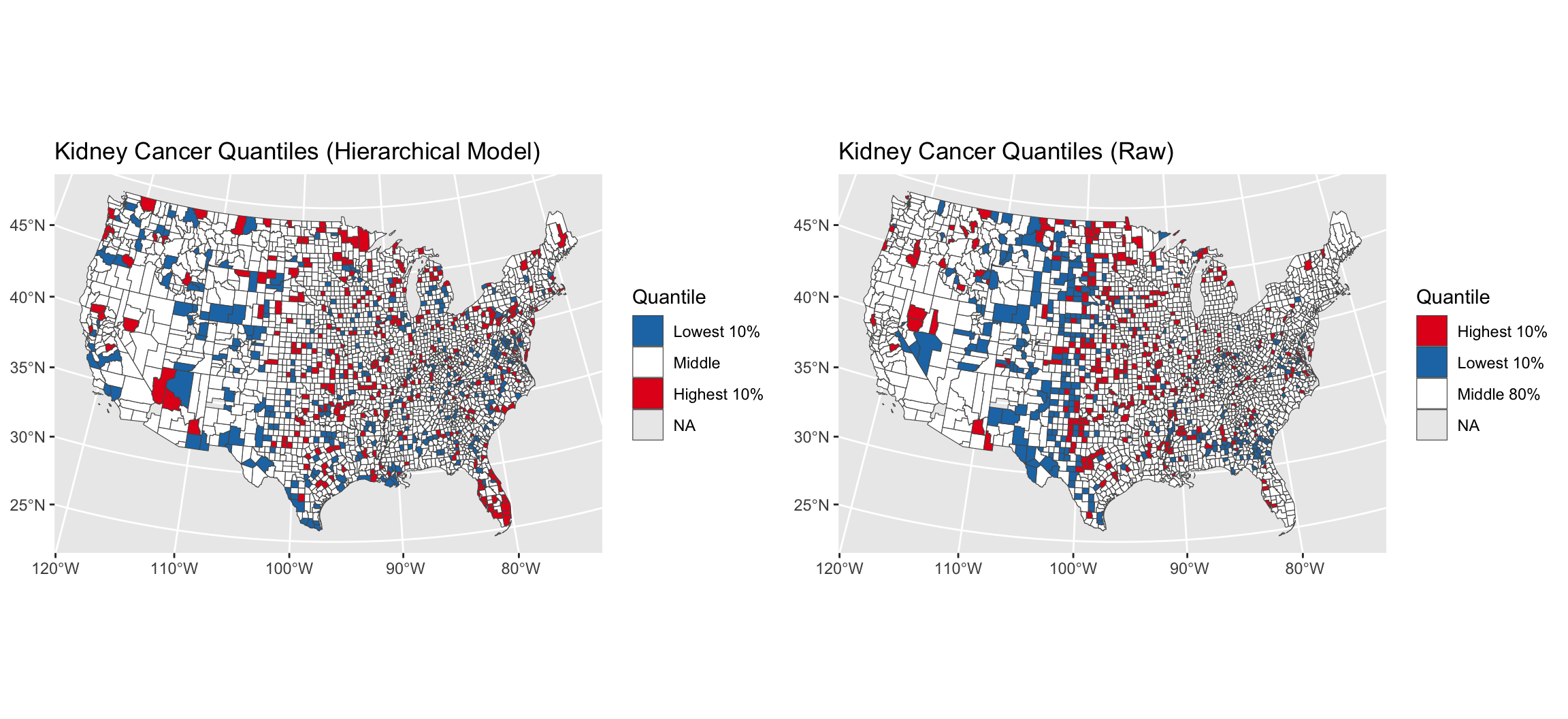
Kidney cancer death rates in the US
- Kidney cancer death rates in the US, by county
- Is there a geographic pattern? If so, why?
Data source: Gelman et al. 2004. Bayesian Data Analysis.
Lauren Talluto
05.12.2024
Data source: Gelman et al. 2004. Bayesian Data Analysis.

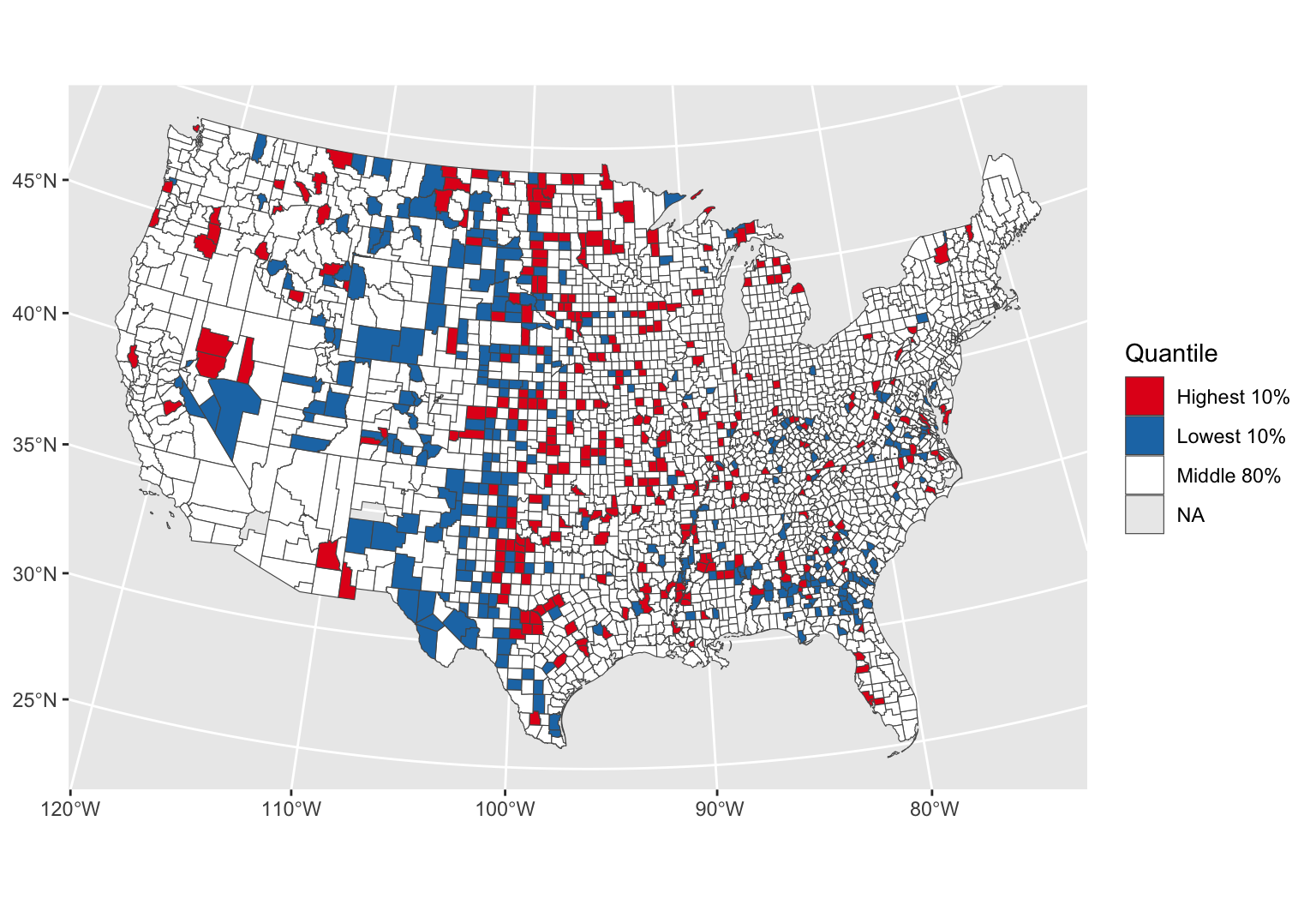
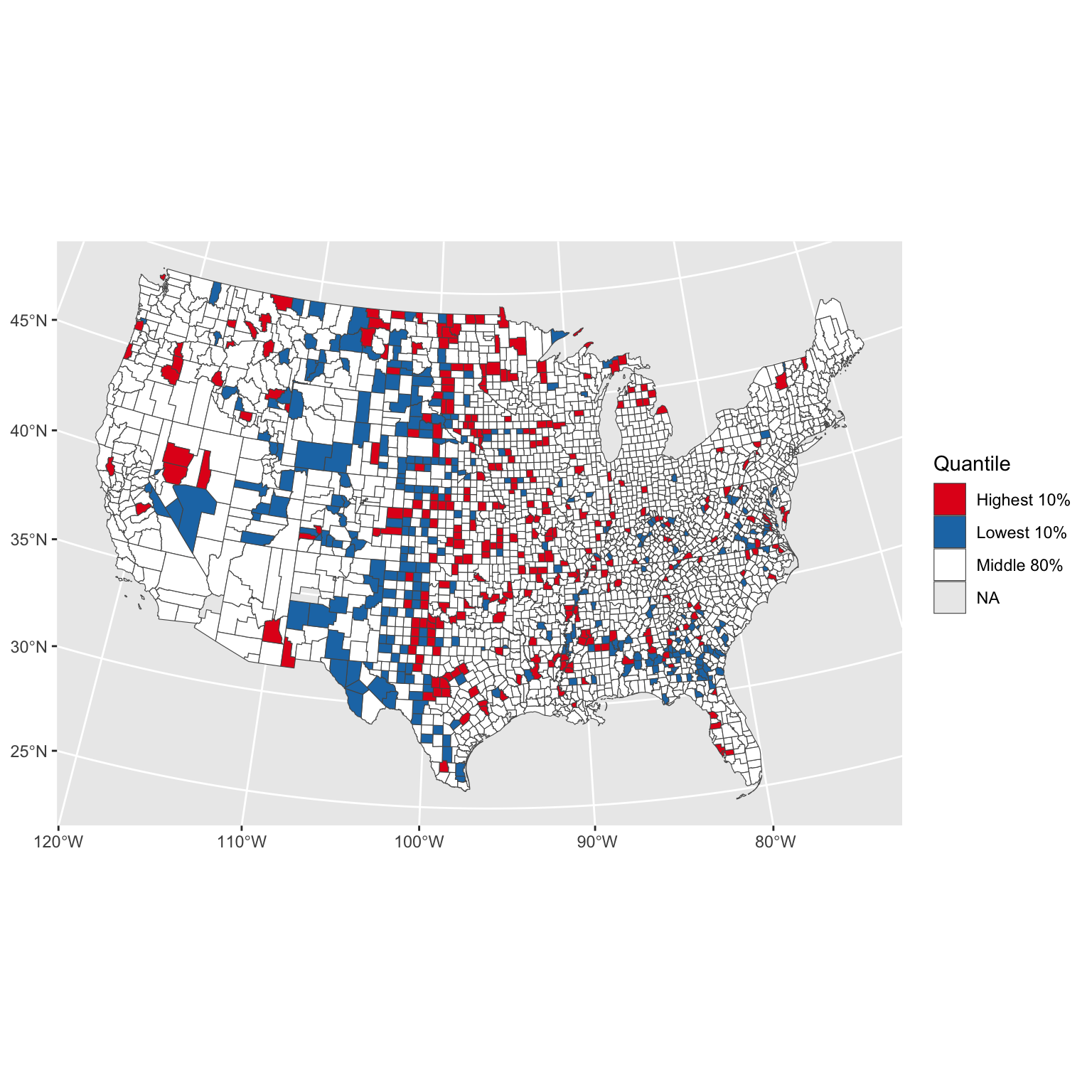
| Highest 10% | 32328 |
| Lowest 10% | 22125 |
| Middle 80% | 208246 |
library(data.table)
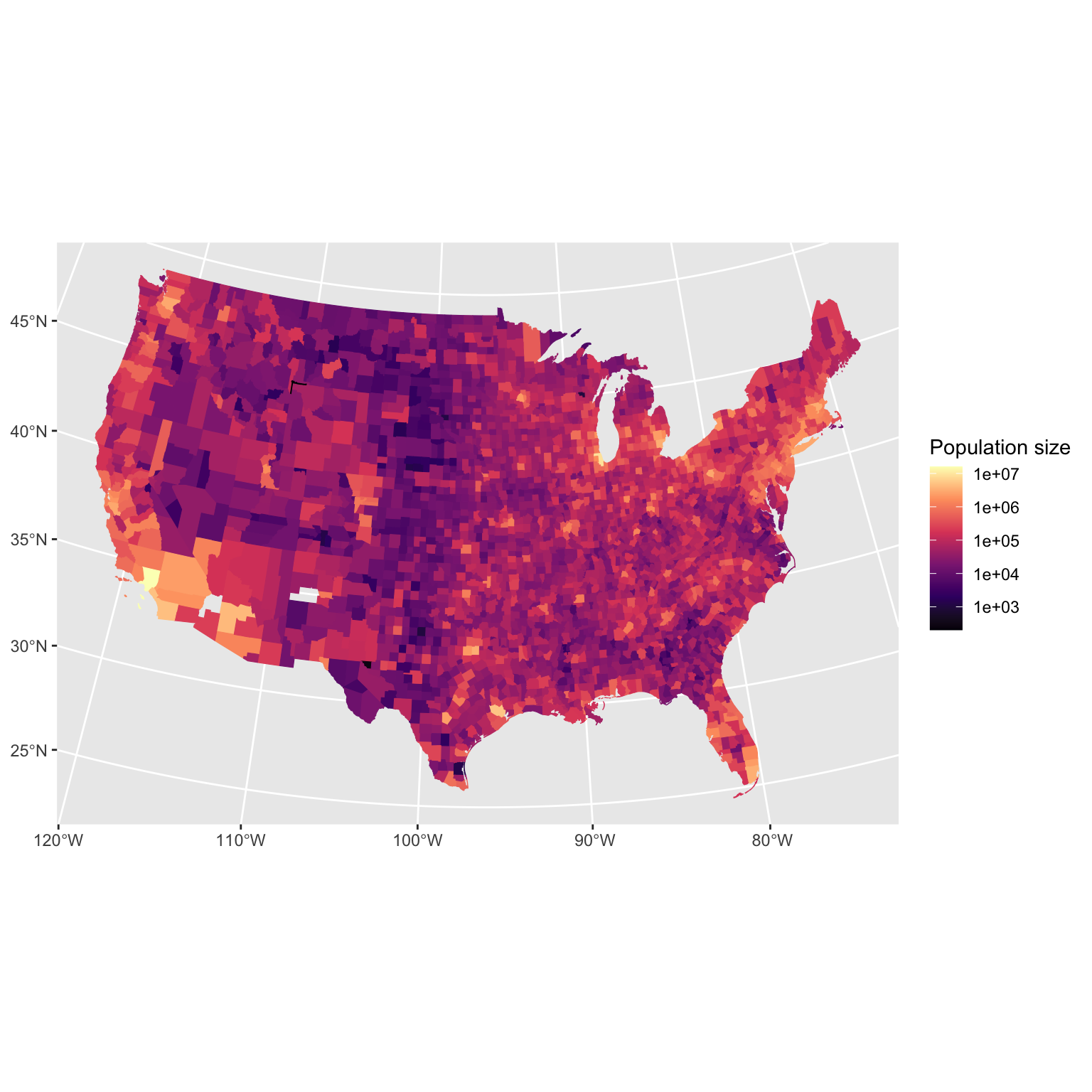
(cancer = readRDS("../vu_advstats_students/data/us_k_cancer.rds"))
## state county kidney_cancer_deaths population death_rate_per_1000
## <char> <char> <int> <int> <num>
## 1: alabama autauga 2 61921 0.03229922
## 2: alabama baldwin 7 170945 0.04094884
## 3: alabama barbour 0 33316 0.00000000
## 4: alabama bibb 0 30152 0.00000000
## 5: alabama blount 3 88342 0.03395893
## ---
## 6256: wyoming sweetwater 2 104192 0.01919533
## 6257: wyoming teton 0 26751 0.00000000
## 6258: wyoming uinta 1 52910 0.01890002
## 6259: wyoming washakie 2 22814 0.08766547
## 6260: wyoming weston 0 17802 0.00000000data {
int <lower = 1> n;
int <lower = 0> deaths [n];
int <lower = 0> population [n];
real <lower = 0> alpha;
real <lower = 0> beta;
}
transformed data {
// cancer is rare, lets make the numbers more reasonable
vector <lower = 0> [n] exposure;
for(i in 1:n)
exposure[i] = population[i] / 1000.0;
}
parameters {
real <lower = 0> lambda;
}
model {
deaths ~ poisson(exposure * lambda);
lambda ~ gamma(alpha, beta);
}Question: Is there geographic variation in cancer rates?
cancer = cancer[complete.cases(cancer)]
cancer_data_stan = list(
n = nrow(cancer),
deaths = cancer$kidney_cancer_deaths,
population = cancer$population,
alpha = 0.01, # extremely vague priors, probably too vague!
beta = 0.01
)
cancer_p_fit = sampling(cancer_pooled, data = cancer_data_stan, refresh = 0)
quantile(as.matrix(cancer_p_fit, pars = "lambda")[,1], c(0.05, 0.95))
## 5% 95%
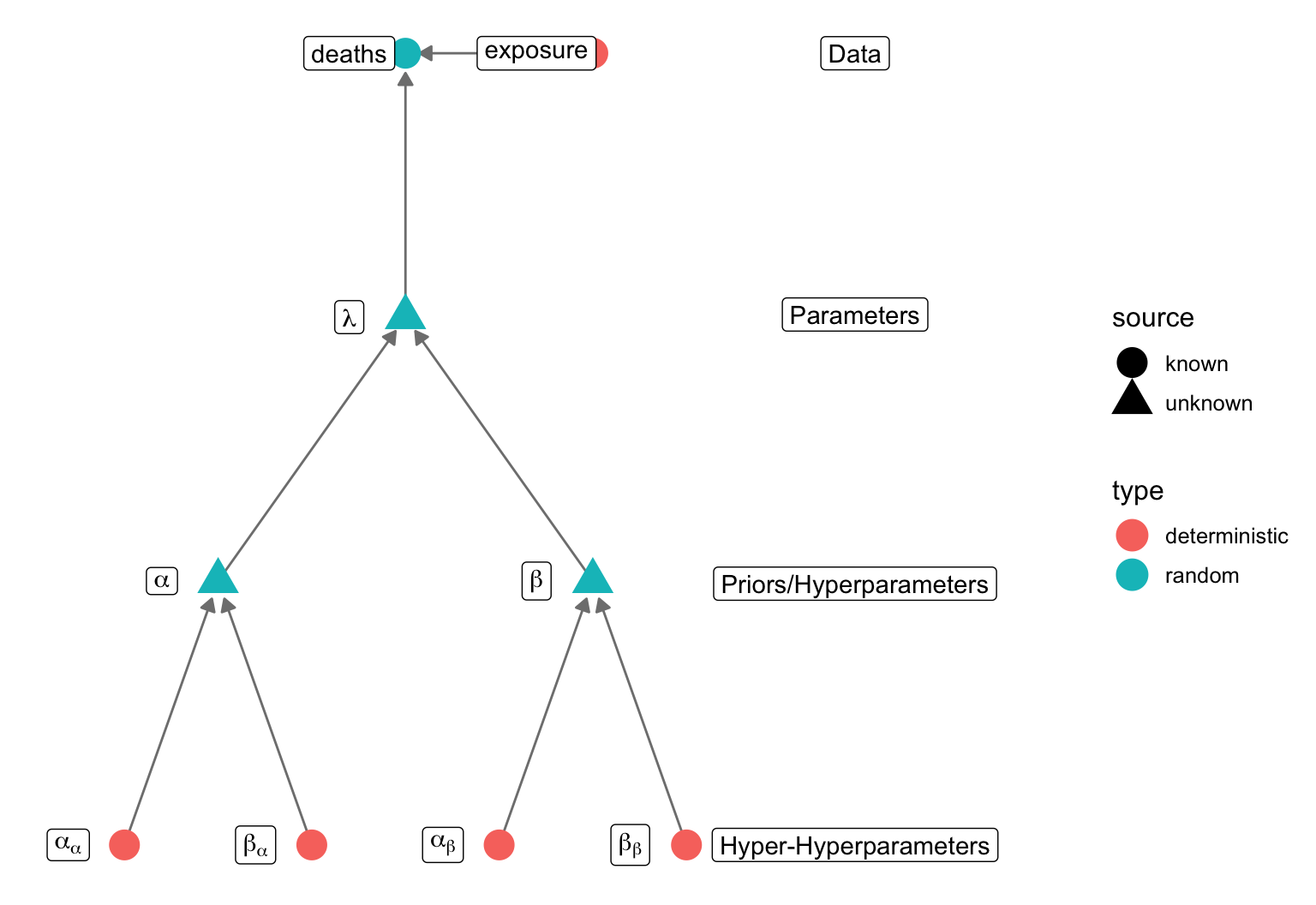
## 0.04989804 0.05064181data {
int <lower = 1> n;
int <lower = 1> n_counties;
int <lower = 0> deaths [n];
int <lower = 0> population [n];
int <lower = 0, upper = n_counties> county_id [n];
real <lower = 0> alpha;
real <lower = 0> beta;
}
transformed data {
// cancer is rare, lets make the numbers more reasonable
vector <lower = 0> [n] exposure;
for(i in 1:n)
exposure[i] = population[i] / 1000.0;
}
parameters {
vector <lower = 0> [n_counties] lambda;
}
model {
for(i in 1:n) {
int j = county_id[i];
deaths[i] ~ poisson(exposure[i] * lambda[j]);
}
lambda ~ gamma(alpha, beta);
}
data {
int <lower = 1> n;
int <lower = 1> n_counties;
int <lower = 0> deaths [n];
int <lower = 0> population [n];
int <lower = 0, upper = n_counties> county_id [n];
// hyper-hyper parameters, for the hyperprior
real <lower = 0> a_alpha;
real <lower = 0> a_beta;
real <lower = 0> b_alpha;
real <lower = 0> b_beta;
}
transformed data {
// cancer is rare, lets make the numbers more reasonable
vector <lower = 0> [n] exposure;
for(i in 1:n)
exposure[i] = population[i] / 1000.0;
}
parameters {
vector <lower = 0> [n_counties] lambda;
// prior hyperparameters for lambda are now parameters we will estimate!
real <lower = 0> alpha;
real <lower = 0> beta;
}
model {
for(i in 1:n) {
int j = county_id[i];
deaths[i] ~ poisson(exposure[i] * lambda[j]);
}
// prior for lambda
lambda ~ gamma(alpha, beta);
// hyperpriors for alpha and beta
alpha ~ gamma(a_alpha, a_beta);
beta ~ gamma(b_alpha, b_beta);
}
generated quantities {
// save the overal mean and variance in cancer rate
real lambda_mu = alpha/beta;
real lambda_var = alpha/beta^2;
}mean(cancer$death_rate_per_1000/(cancer$population/1000))
## [1] 0.00214512
sd(cancer$death_rate_per_1000/(cancer$population/1000))
## [1] 0.009377513
alpha_a = 0.01
beta_a = 1
# our hyperparameter alpha has a 99% prob of being between these two values
(a_int = qgamma(c(0.01, 0.99), alpha_a, beta_a))
## [1] 5.660738e-201 2.650526e-01
alpha_b = 0.8
beta_b = 0.4
# our hyperparameter beta has a 99% prob of being between these two values
(b_int = (round(qgamma(c(0.01, 0.99), alpha_b, beta_b), 2)))
## [1] 0.01 10.32
## what would the mean lambda look like at these extremes?
round(matrix(c(a_int[1] / b_int[1], a_int[2]/b_int[1], a_int[1] / b_int[2], a_int[2] / b_int[2]), nrow = 2,
dimnames = list(c("min a", "max a"), c("min b", "max b"))),2)
## min b max b
## min a 0.00 0.00
## max a 26.51 0.03
cancer_data_stan$a_alpha = alpha_a
cancer_data_stan$b_alpha = alpha_b
cancer_data_stan$a_beta = beta_a
cancer_data_stan$b_beta = beta_bcancer$county_id = as.integer(factor(cancer$county))
cancer_data_stan$county_id = cancer$county_id
cancer_data_stan$n_counties = max(cancer$county_id)
cancer_ppool_fit = sampling(cancer_ppooled, data = cancer_data_stan, refresh = 0, iter = 5000)
cancer_ppool_samps = as.matrix(cancer_ppool_fit, pars = "lambda")
quants = t(apply(cancer_ppool_samps , 2, quantile, c(0.05, 0.95)))
head(quants)
##
## parameters 5% 95%
## lambda[1] 0.04898104 0.10210214
## lambda[2] 0.05070926 0.09266323
## lambda[3] 0.04553328 0.09471457
## lambda[4] 0.03329695 0.05399416
## lambda[5] 0.03806352 0.07241783
## lambda[6] 0.03656477 0.04935245
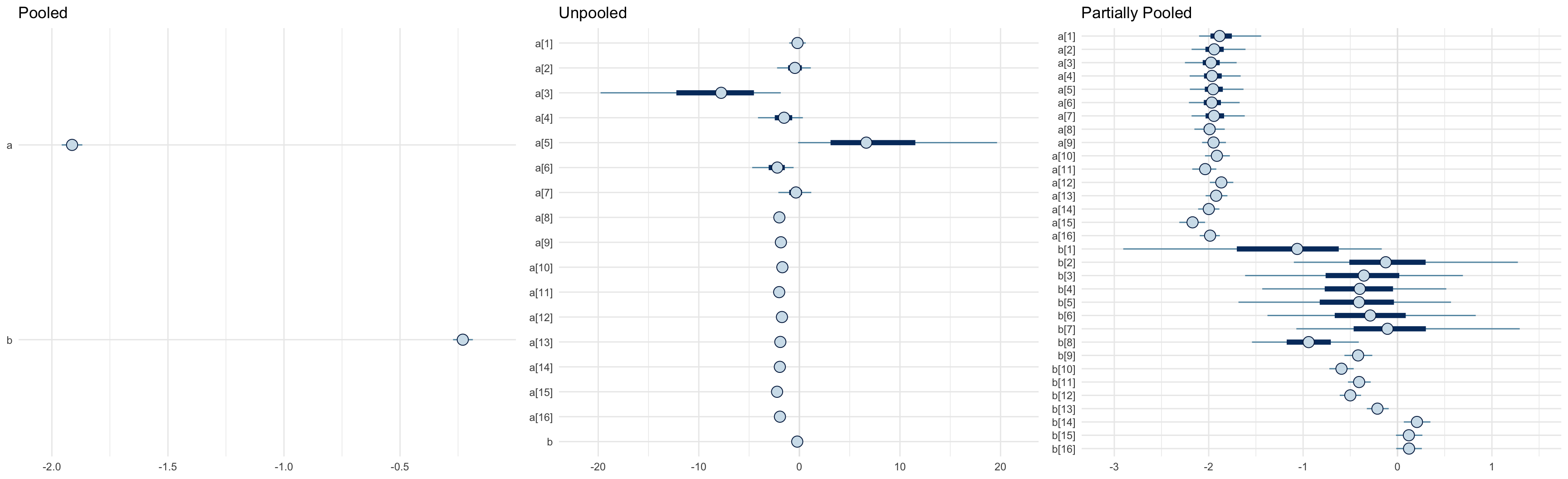
# quantile interval for the overall mean
round(rbind(pooled = quantile(as.matrix(cancer_p_fit, pars = "lambda"), c(0.05, 0.95)),
partial_pooled = quantile(as.matrix(cancer_ppool_fit, pars = "lambda_mu"), c(0.05, 0.95))), 4)
## 5% 95%
## pooled 0.0499 0.0506
## partial_pooled 0.0508 0.0527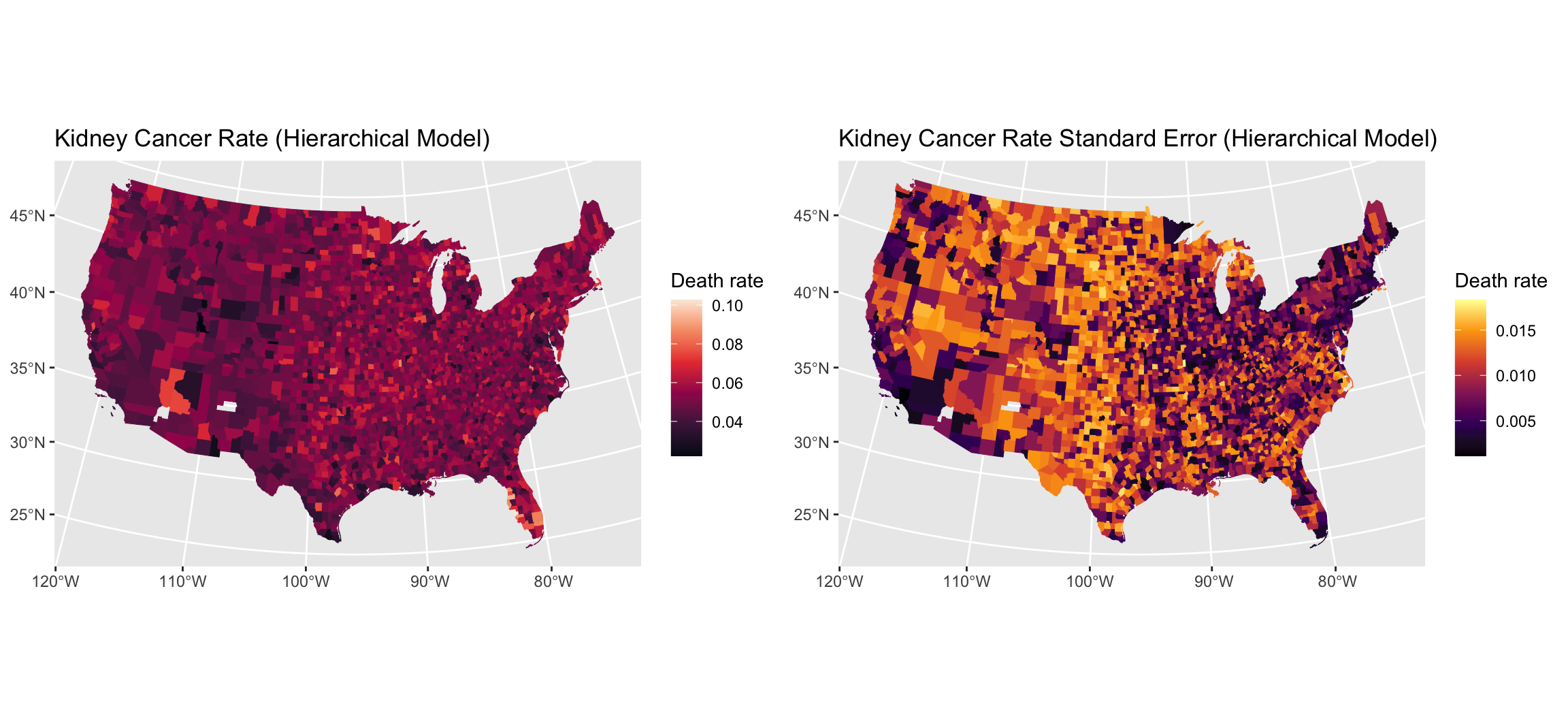
trees = fread("../vu_advstats_students/data/treedata.csv")
tsuga = trees[grep("Tsuga", species_name)]
# remove NAs
tsuga = tsuga[complete.cases(tsuga), ]
head(tsuga)
## n died year species_name annual_mean_temp tot_annual_pp prior_mu
## <int> <int> <int> <char> <num> <num> <num>
## 1: 5 3 1989 Tsuga canadensis 3.849333 1003.0000 0.02222166
## 2: 6 0 1989 Tsuga canadensis 3.452000 1076.1333 0.02222166
## 3: 3 0 1997 Tsuga canadensis 3.620000 1099.4000 0.03245619
## 4: 4 4 1989 Tsuga canadensis 4.596000 989.4667 0.02222166
## 5: 3 0 1994 Tsuga canadensis 4.244667 1116.2000 0.02816339
## 6: 7 0 2002 Tsuga canadensis 4.730000 1137.2667 0.04108793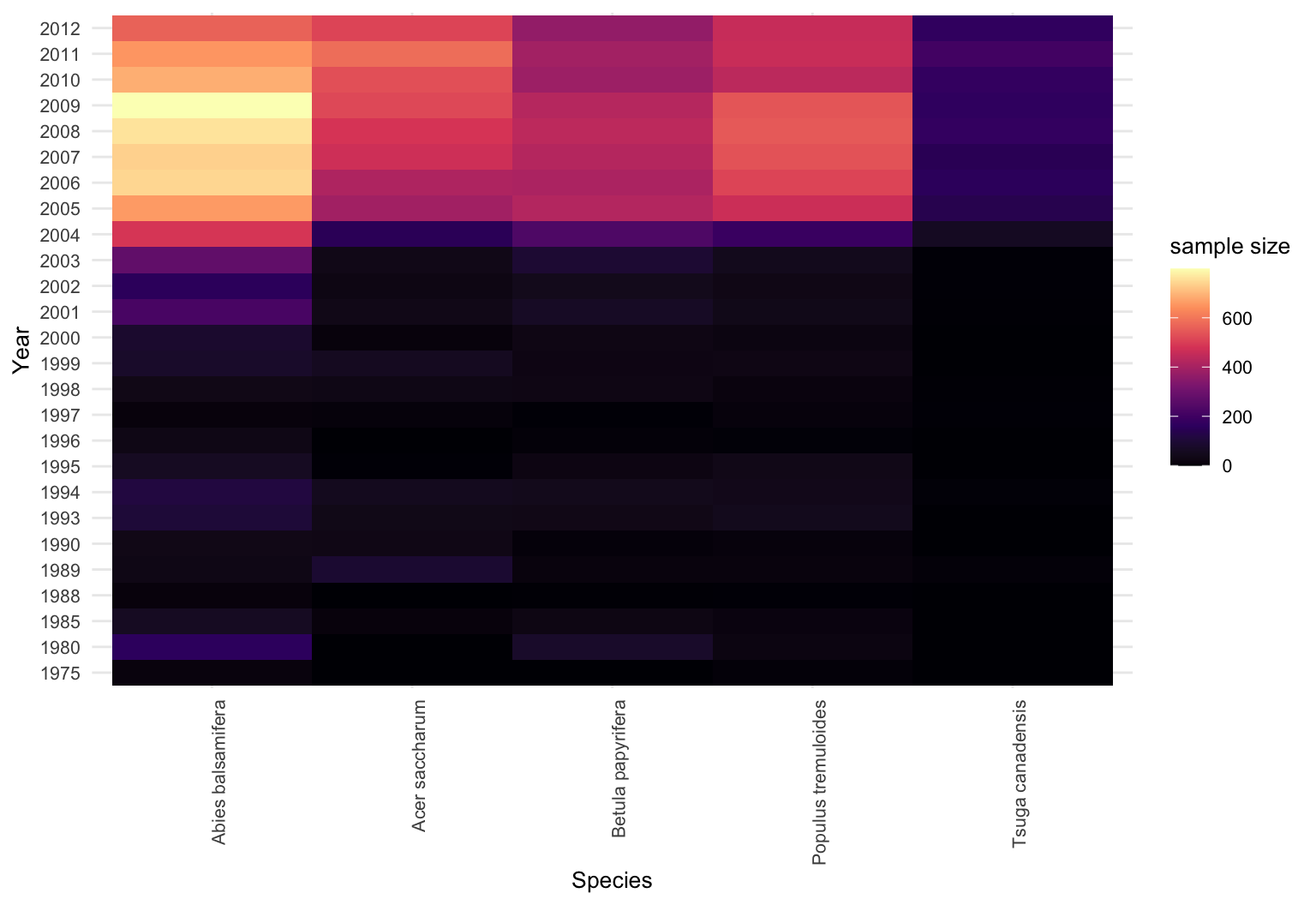
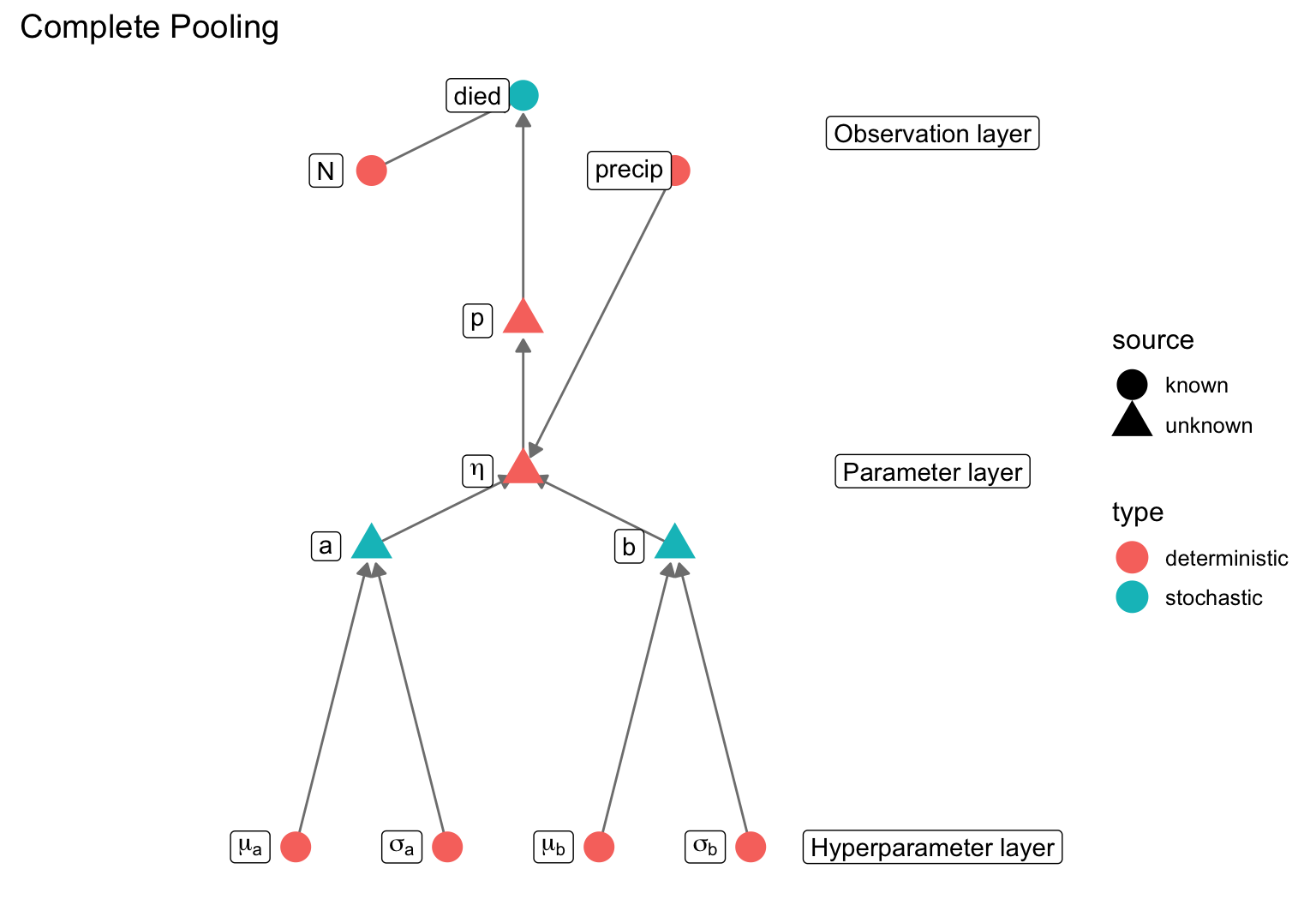
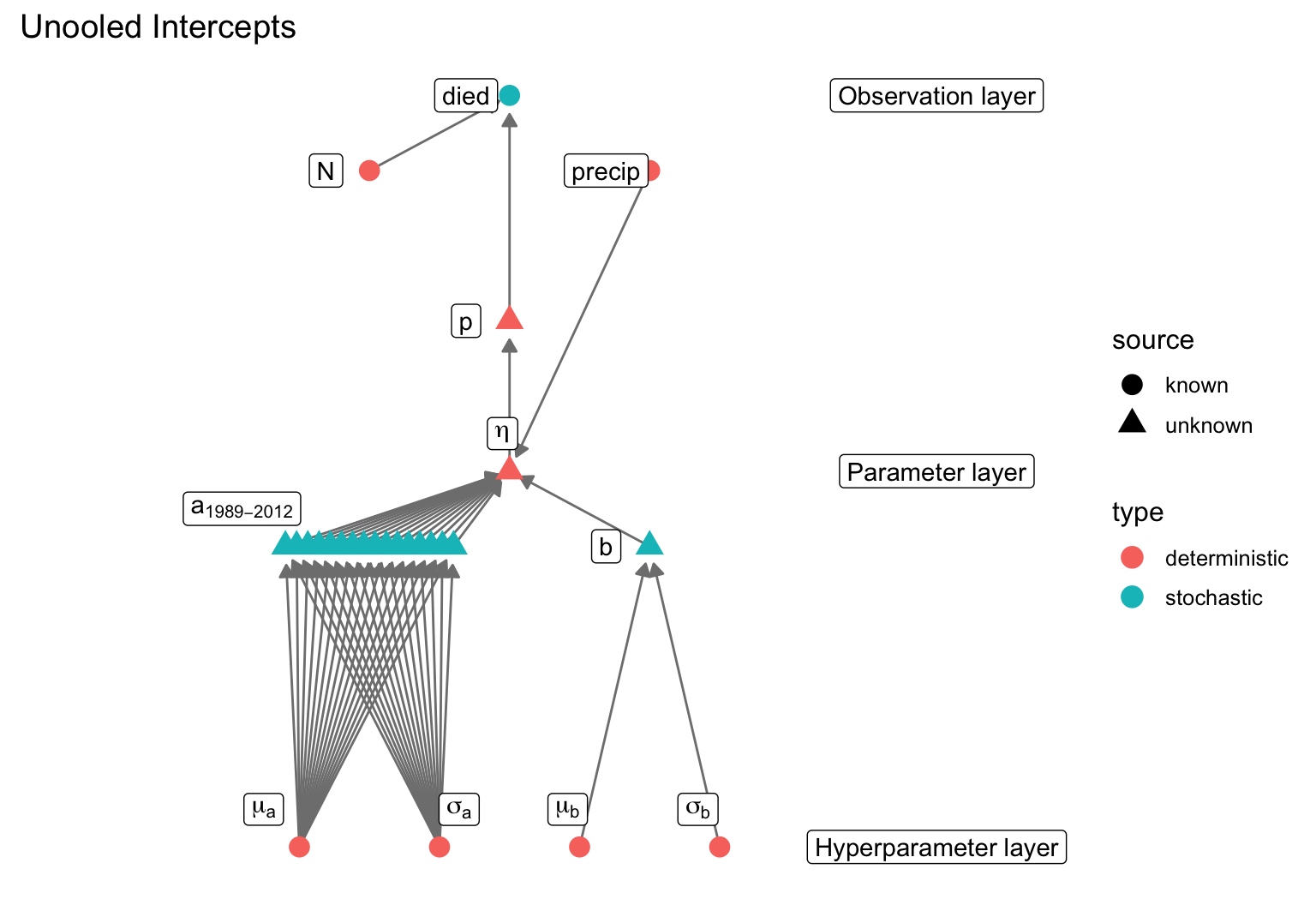
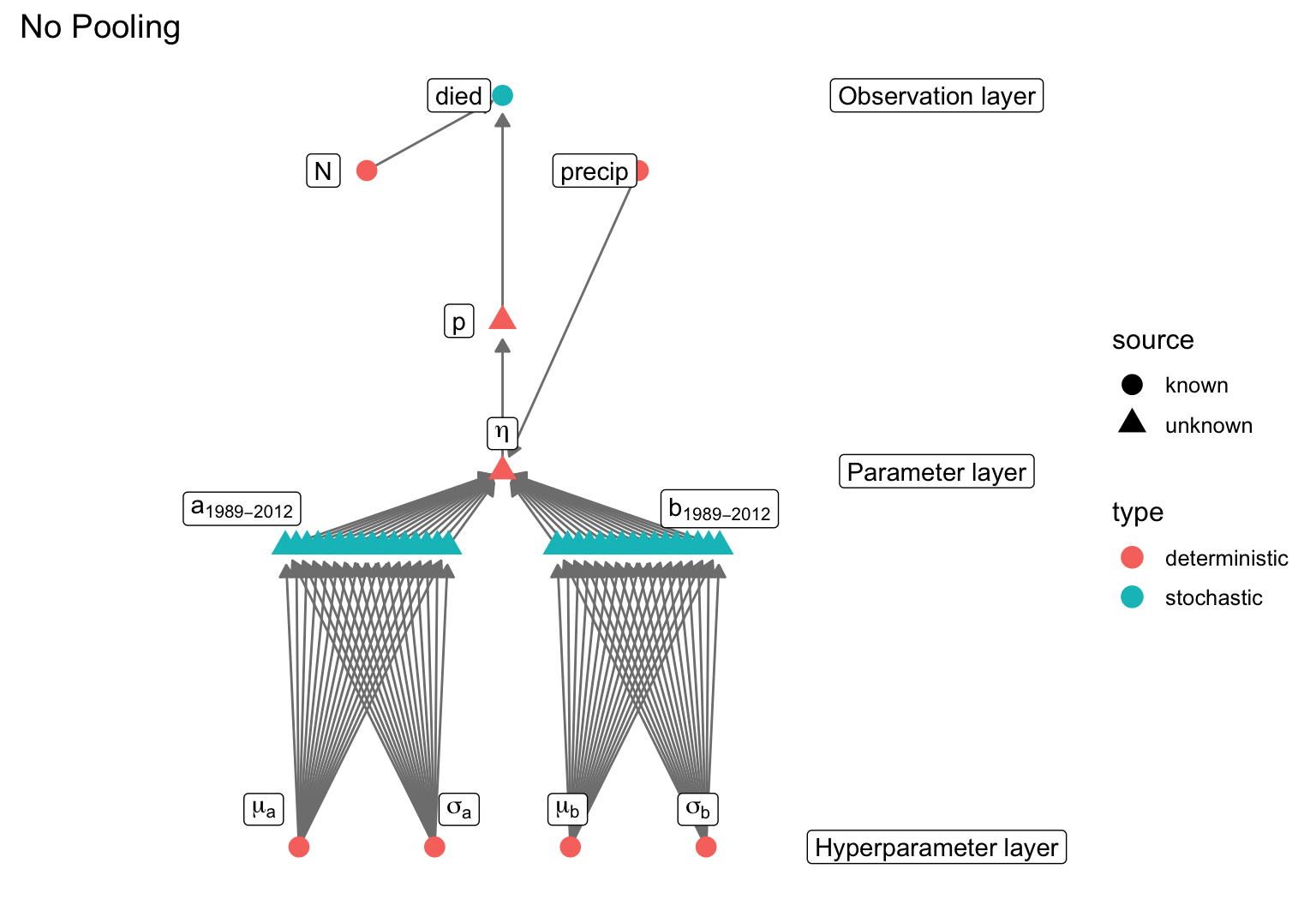
data {
// number of data points
int <lower=0> n;
// number of trees in each plot
int <lower=1> n_trees [n];
// number died
int <lower=0> died [n];
vector [n] precip;
}
parameters {
real a;
real b;
}
transformed parameters {
vector <lower=0, upper=1> [n] p;
p = inv_logit(a + b * precip);
}
model {
died ~ binomial(n_trees, p);
a ~ normal(0, 10);
b ~ normal(0, 5);
}
generated quantities {
// we use generated quantities to keep track of log likelihood and
// deviance, useful for model selection
// and also to perform poserior predictive simulations
real deviance = 0;
vector [n] loglik;
int ppd_died [n];
for (i in 1:n) {
loglik[i] = binomial_lpmf(died[i] | n_trees[i], p[i]);
deviance += loglik[i];
ppd_died[i] = binomial_rng(20, p[i]);
}
deviance = -2 * deviance;
}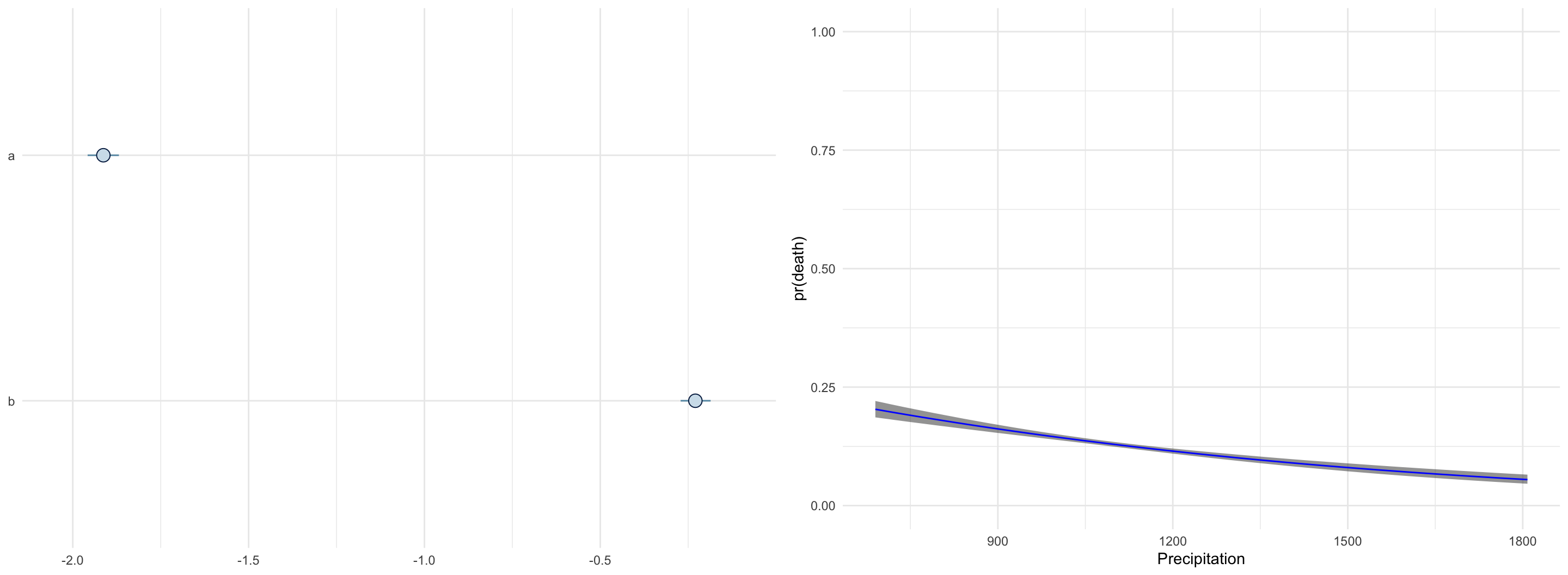
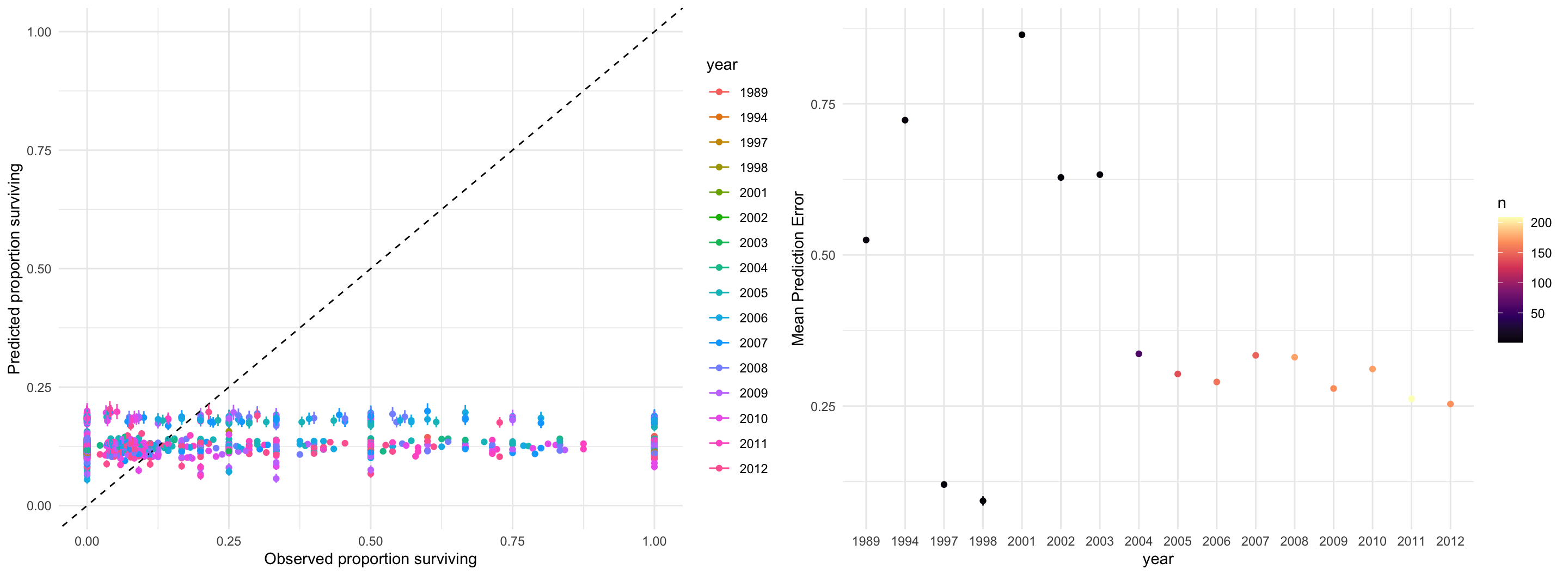
data {
// not the complete program, only differences from pooled model
// grouping variables
// year_id is an integer starting at 1 (the earliest year)
// ending at n_groups (the latest year)
// we use this value as an index for any group-level effects
int <lower=1> n_groups;
int <lower=1, upper = n_groups> year_id [n];
}
parameters {
// one intercept per group
vector [n_groups] a;
}
transformed parameters {
// a is different for each data point, depending on the group
// so we need a loop to compute this
for(i in 1:n) {
int gid = year_id[i];
p[i] = inv_logit(a[gid] + b * precip[i]);
}
}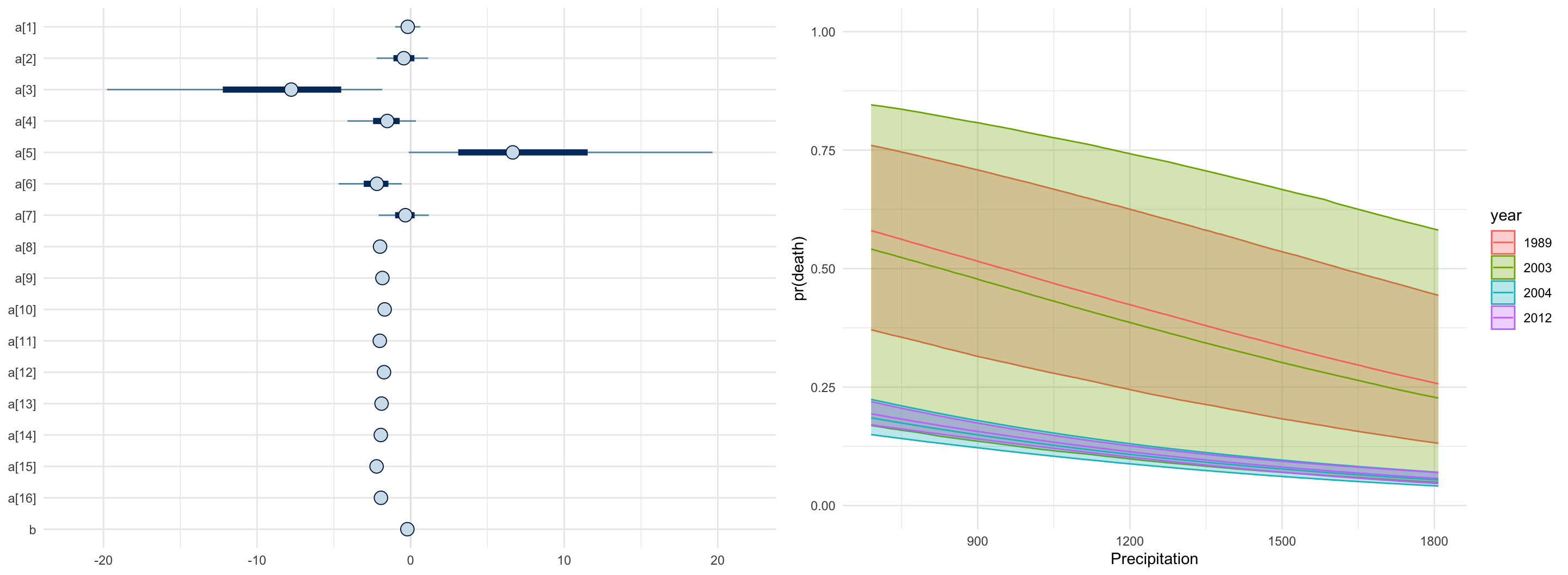
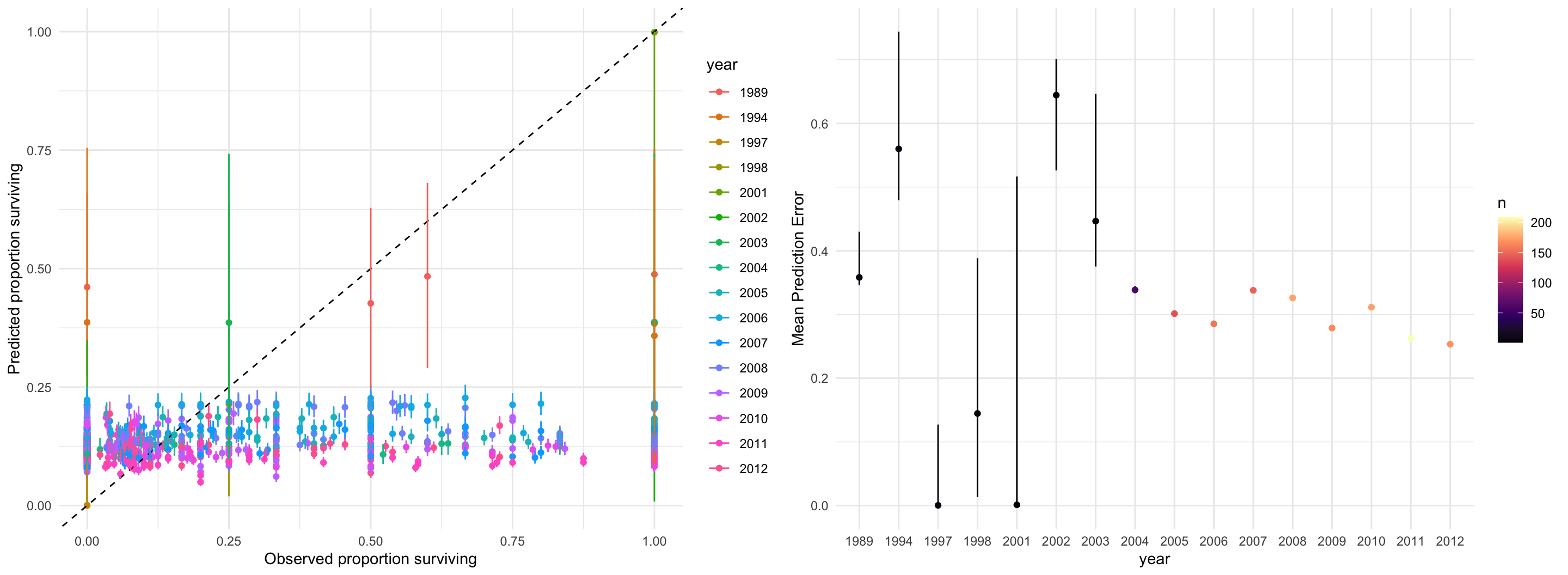
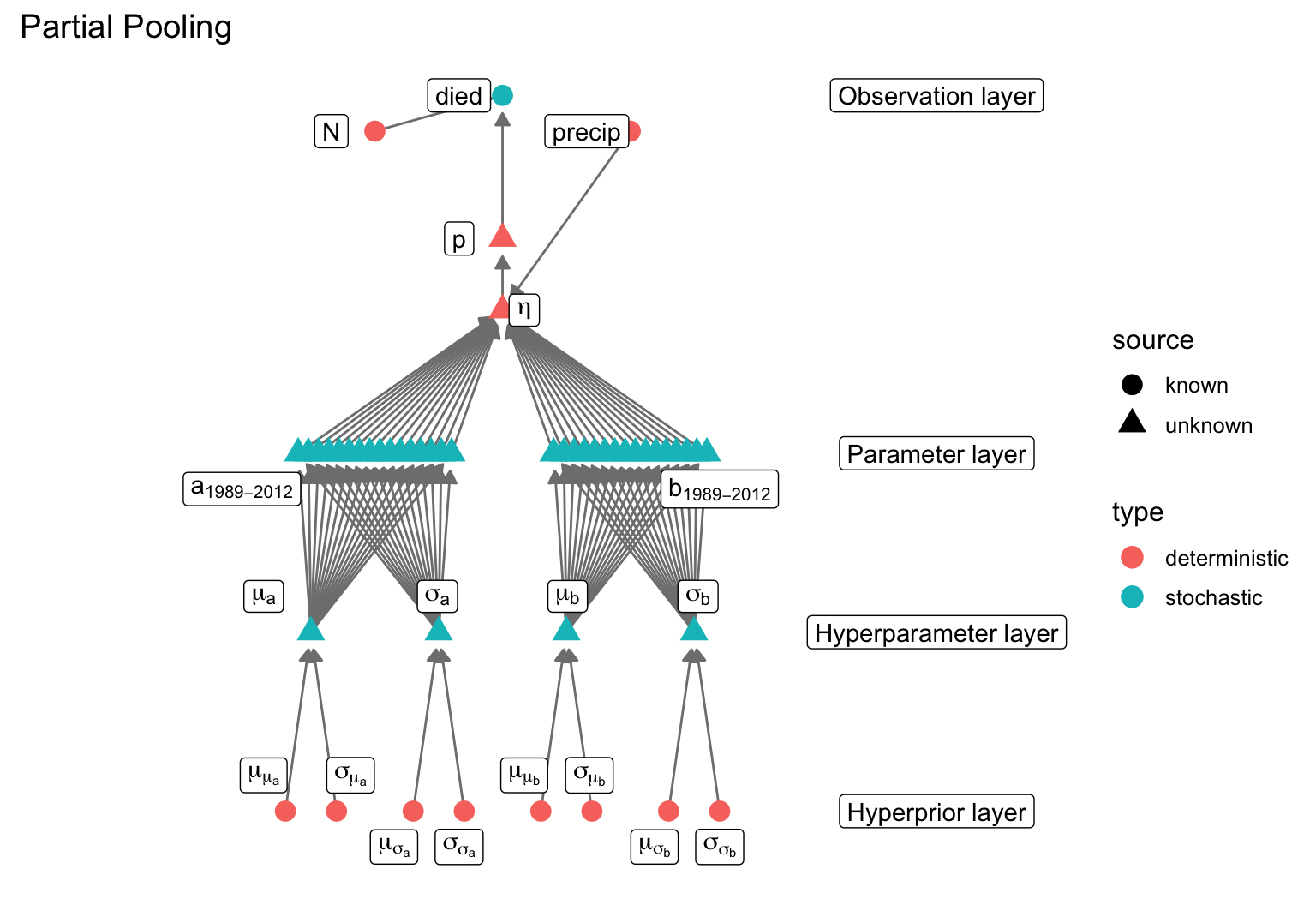
data {
// not the complete program, only differences from pooled model
// grouping variables
// year_id is an integer starting at 1 (the earliest year)
// ending at n_groups (the latest year)
// we use this value as an index for any group-level effects
int <lower=1> n_groups;
int <lower=1, upper = n_groups> year_id [n];
}
parameters {
// one intercept and one slope per group
vector [n_groups] a;
vector [n_groups] b;
// hyperparameters describe higher-level structure in the data
// in this case both the a's and b's come from populations
// with their own mean and variance to be estimated from the data
real a_mu;
real <lower=0> a_sig;
real b_mu;
real <lower=0> b_sig;
}
transformed parameters {
for(i in 1:n) {
int gid = year_id[i];
p[i] = inv_logit(a[gid] + b[gid] * precip[i]);
}
}
model {
// The priors are now estimated from the data
a ~ normal(a_mu, a_sig);
b ~ normal(b_mu, b_sig);
// hyperpriors describe what we know about higher (group-level) structure
a_mu ~ normal(0, 20);
b_mu ~ normal(0, 20);
// half cauchy is common for hierarchical stdev
a_sig ~ cauchy(0, 20);
b_sig ~ cauchy(0, 20);
}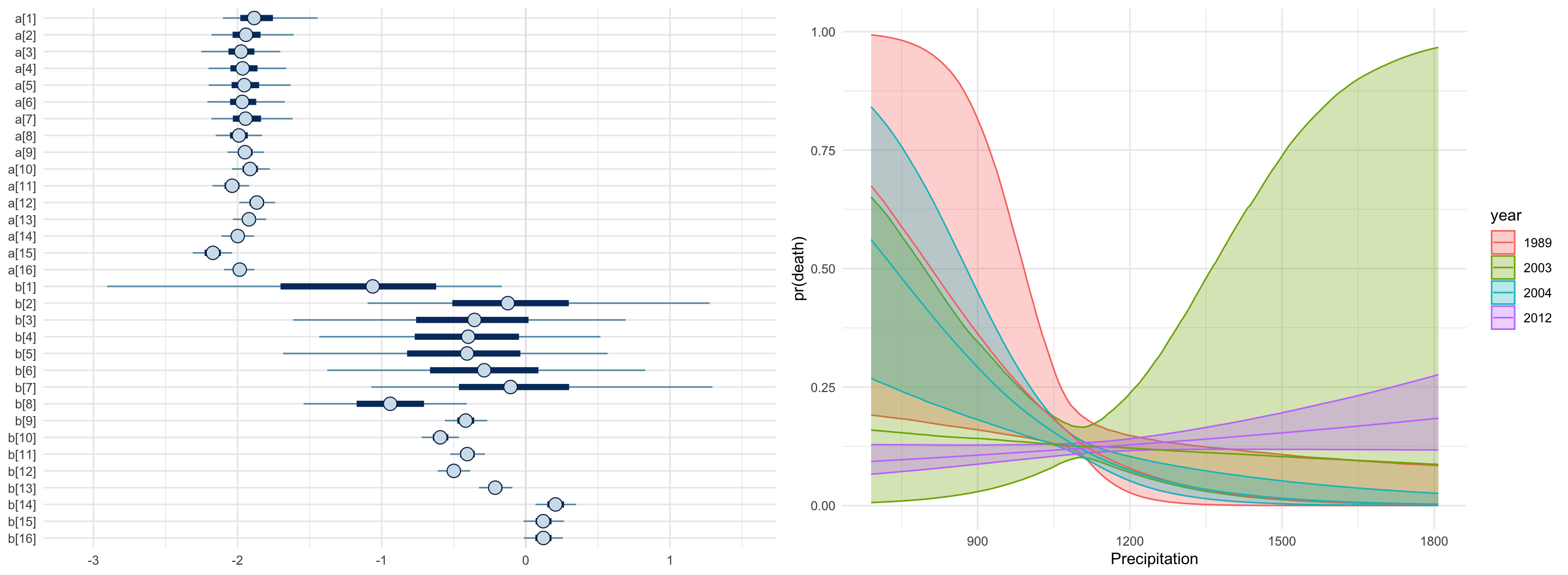
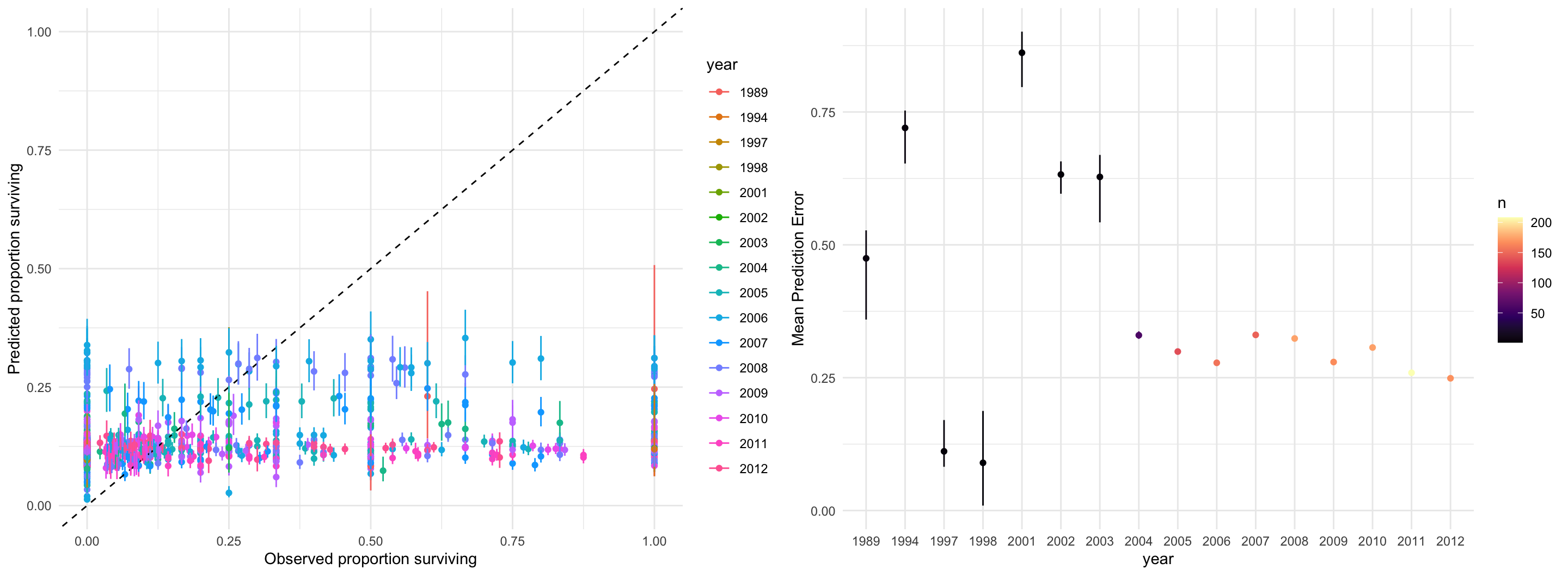
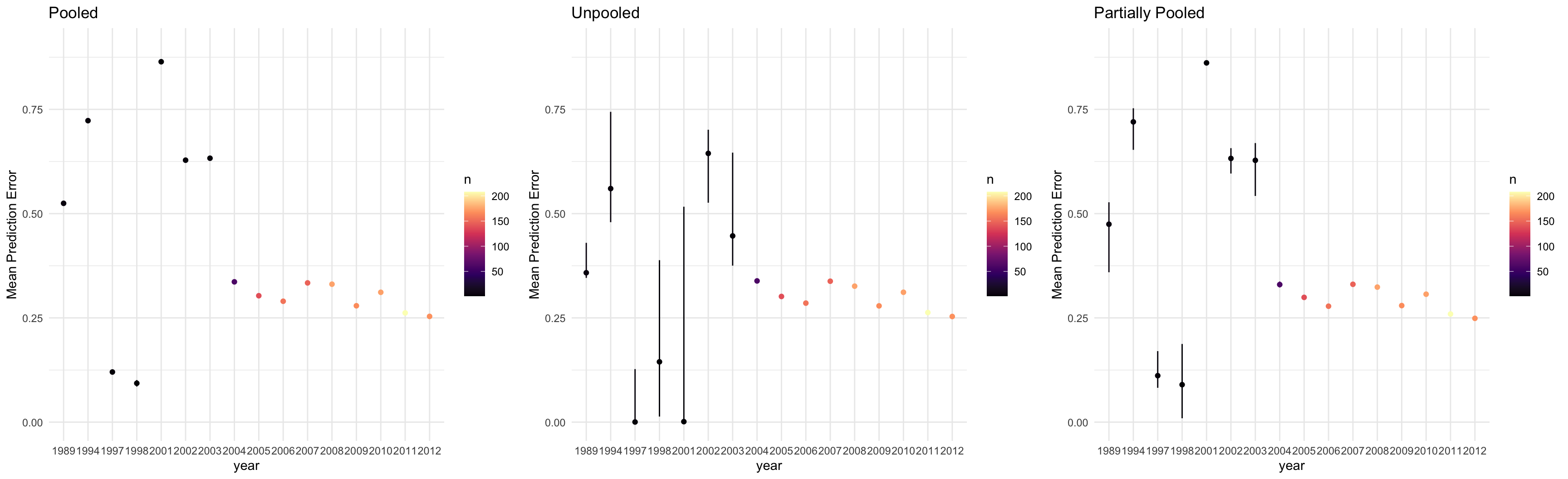
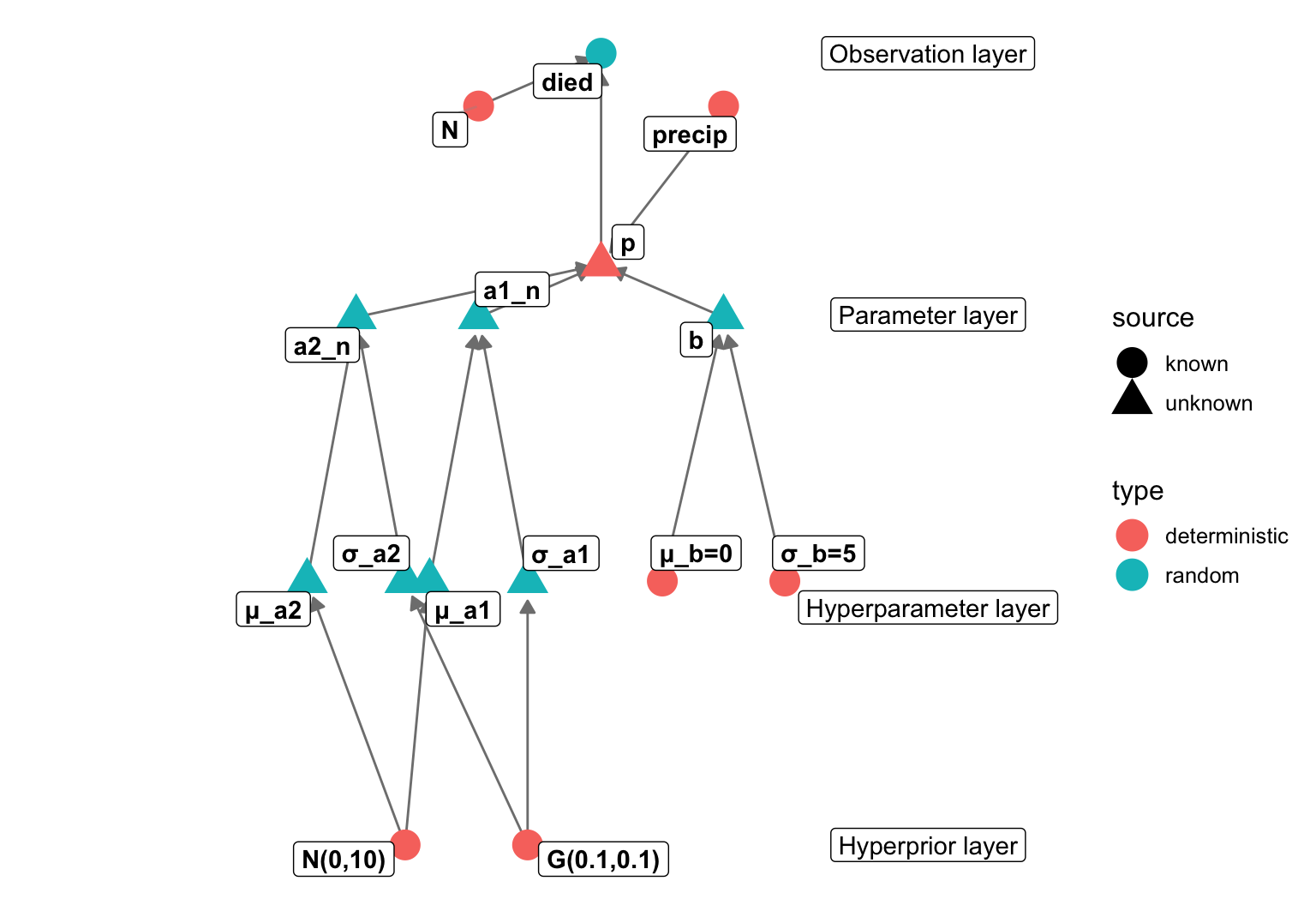
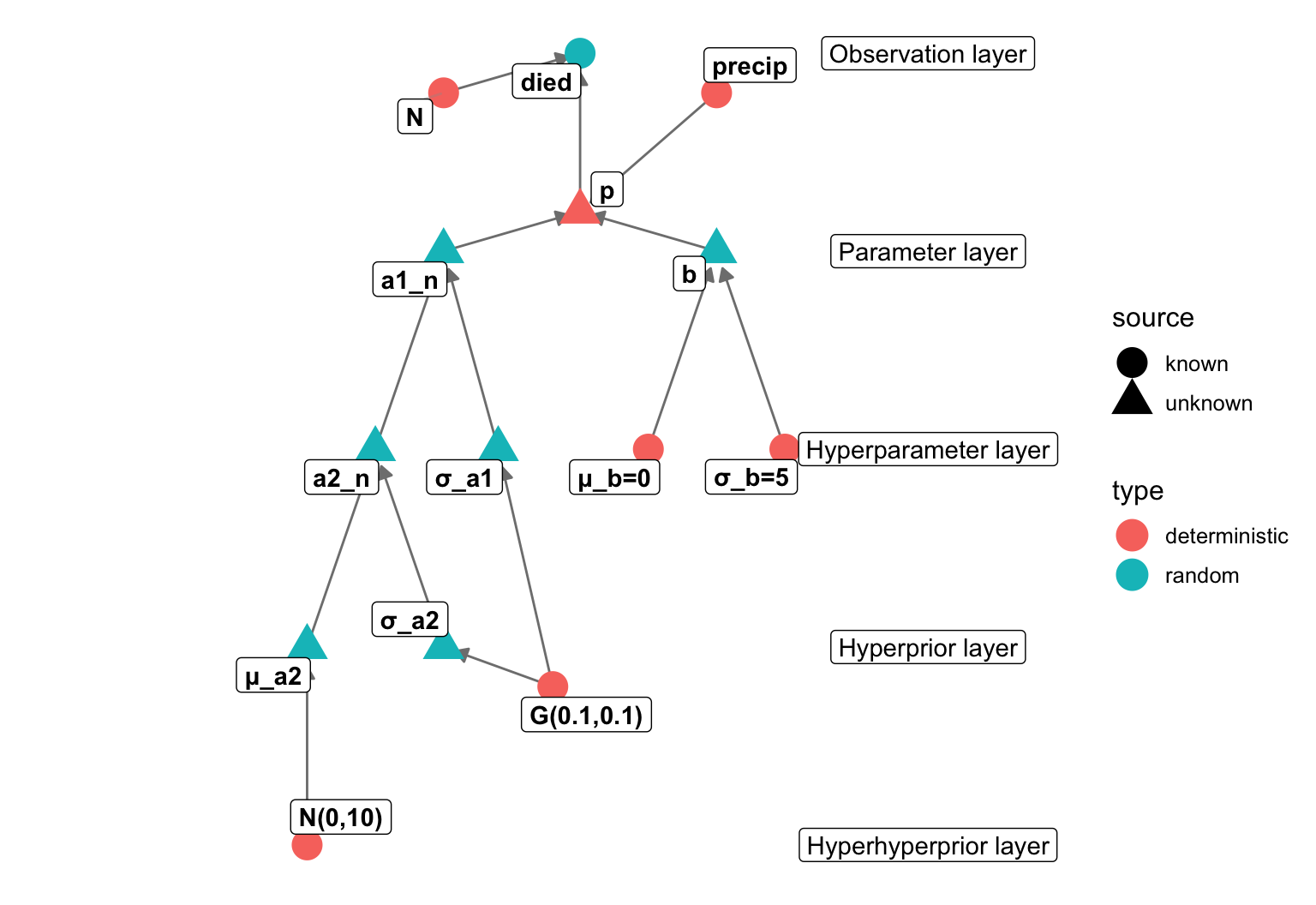
data {
// group-level objects
int <lower=1> n_groups;
int <lower=1, upper=n_groups> group_id [n];
}
parameters {
vector [n_groups] a;
// hyperparameters
real a_mu;
real a_sig;
}
transformed parameters {
pr[i] = inv_logit(a[group_id[i]]);
}
model {
a ~ normal(a_mu, a_sig); // hierarchical prior for a
}
data {
int n; // number of data points
int died [n]
int N[n];
vector [n] precip;
// group-level objects
int <lower=1> n_group1;
int <lower=1, upper=n_group1> group1_id [n];
int <lower=1> n_group2;
int <lower=1, upper=n_group2> group2_id [n];
}
parameters {
vector [n_group1] a1;
vector [n_group2] a2;
// hyperparameters
real a1_mu;
real <lower=0> a1_sig;
real a2_mu;
real <lower=0> a2_sig;
}
transformed parameters {
vector [n] pr;
for(i in 1:n)
pr[i] = inv_logit(a1[group1_id[i]] + a2[group2_id[i]] + b*precip[i]);
}
model {
died ~ binomial(N, pr); // likelihood
a1 ~ normal(a1_mu, a1_sig); // hierarchical prior for a1
a2 ~ normal(a2_mu, a2_sig); // hierarchical prior for a2
// hyperpriors
a1_mu ~ normal(0,10)
a2_mu ~ normal(0,10)
a1_sig ~ gamma(0.1, 0.1);
a2_sig ~ gamma(0.1, 0.1);
}
data {
int n; // number of data points
int died [n]
int N[n];
vector [n] temperature;
// group-level objects
int <lower=1> n_group1;
int <lower=1, upper=n_group1> group1_id [n];
int <lower=1> n_group2;
int <lower=1, upper=n_group2> group2_id [n_group1];
}
parameters {
vector [n_group1] a1;
vector [n_group2] a2;
// hyperparameters
real <lower=0> a1_sig;
real a2_mu;
real <lower=0> a2_sig;
}
transformed parameters {
vector [n] pr;
for(i in 1:n)
pr[i] = inv_logit(a1[group1_id[i]] + b*precip[i]);
}
model {
died ~ binomial(N, pr); // likelihood
for(i in n_group1)
a1 ~ normal(a2[i], a1_sig); // hierarchical prior for a1
// hyperpriors
a2 ~ normal(a2_mu, a2_sig); // hierarchical prior for a2
a1_sig ~ gamma(0.1, 0.1);
// hyperhyperprior
a2_mu ~ normal(0,10)
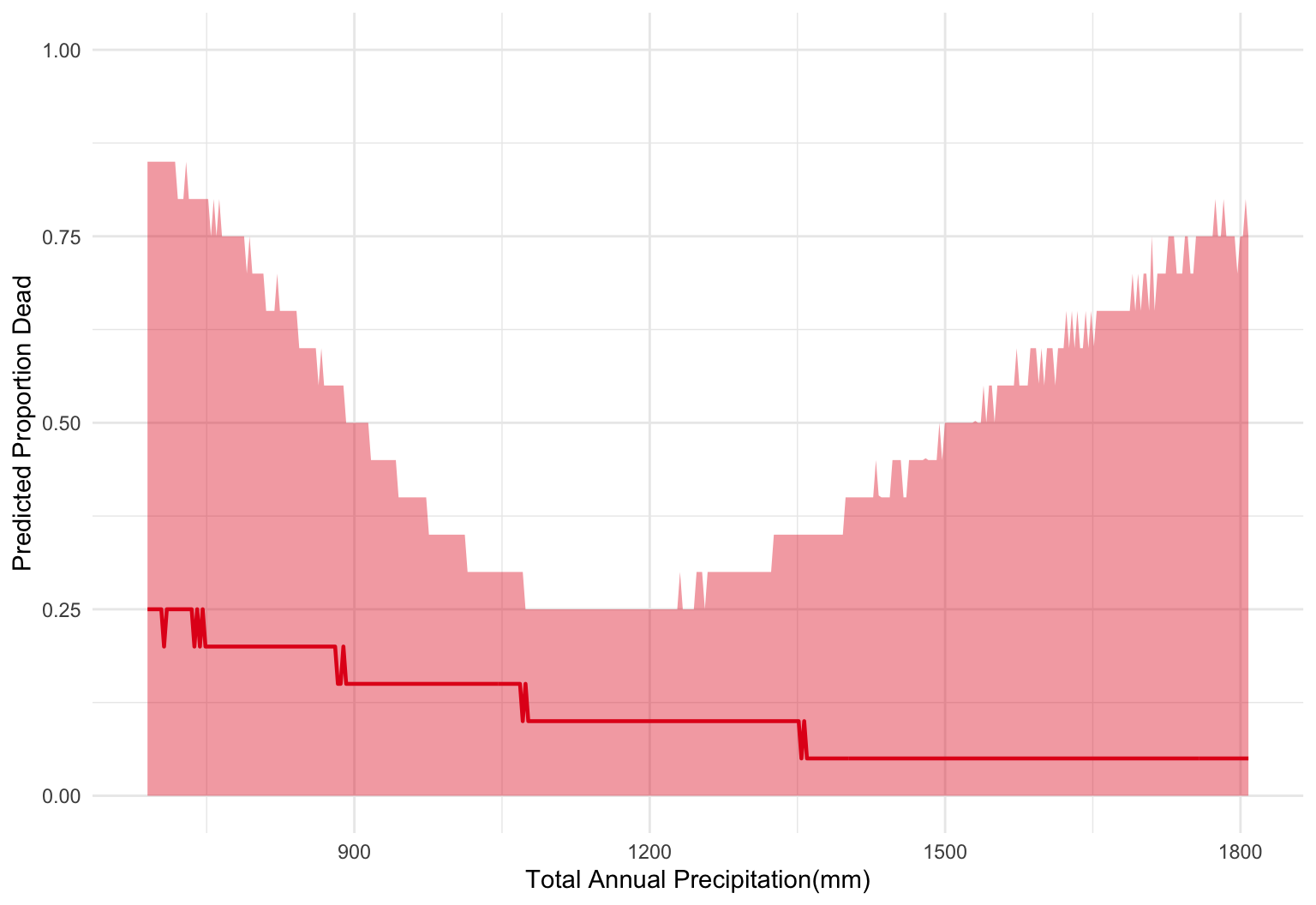
}newx = seq(min(standat$precip), max(standat$precip), length.out=400)
pars = data.frame(as.matrix(fit_ppool, pars=c("a_mu", "a_sig", "b_mu", "b_sig")))
# For our hypothetical, we need to decide how many trees we would see
# more trees means less sampling uncertainty
N = 20
sims = mapply(sim1, amu = pars$a_mu, asig = pars$a_sig,
bmu = pars$b_mu, bsig = pars$b_sig,
MoreArgs = list(N = 20, precip = newx))
sim_quantiles = apply(sims, 1, quantile, c(0.5, 0.05, 0.95))