Chapter 1: An abundance model for Prosopistoma
Indroducing Prosopistoma peregrinum

Nearly extinct, known from only 3 rivers in Europe.
Question: What habitat features are important for maintaining large populations?
Lauren Talluto
12.12.2024
Indroducing Prosopistoma peregrinum


Nearly extinct, known from only 3 rivers in Europe.
Question: What habitat features are important for maintaining large populations?
Question: What habitat features are important for maintaining large populations?
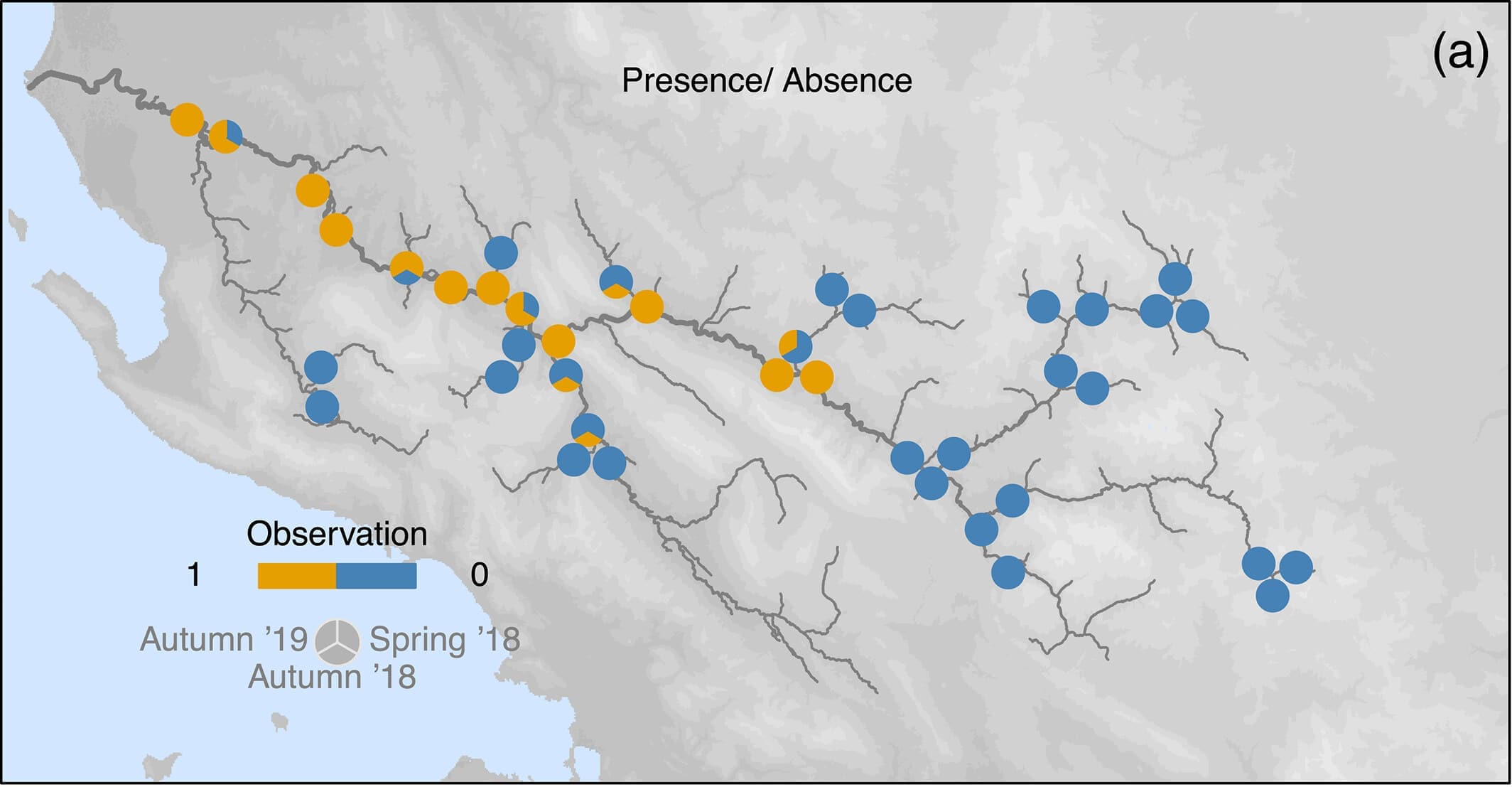
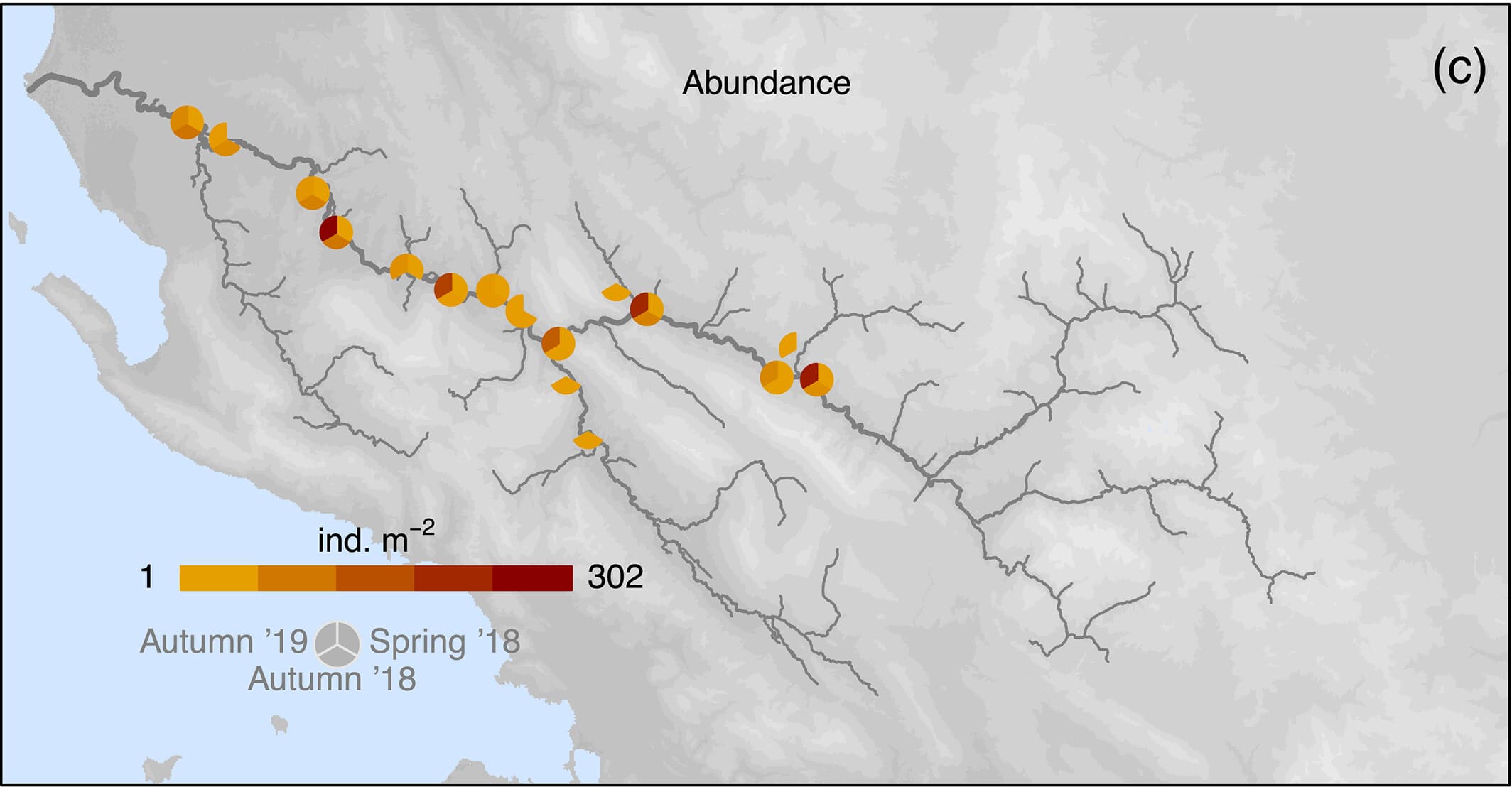
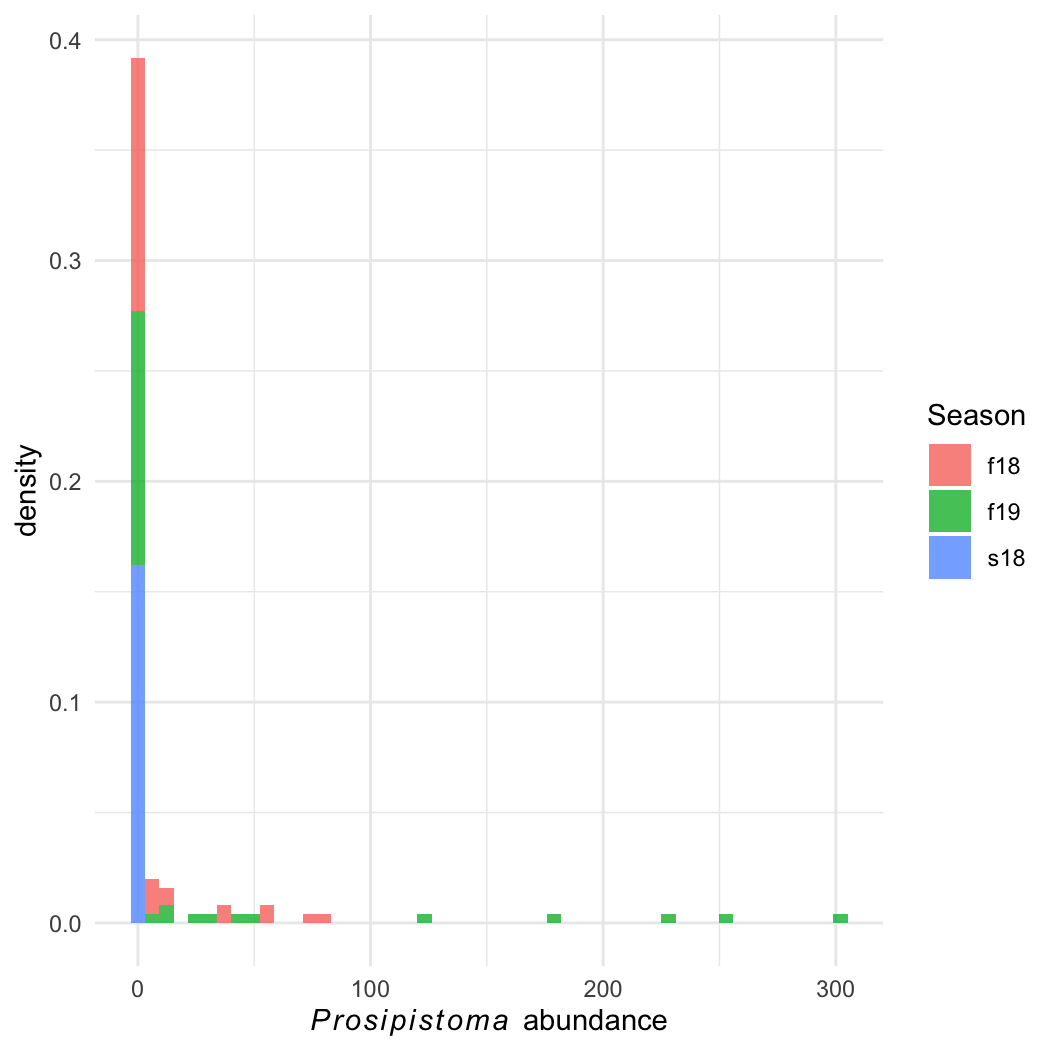
Easier question: What determines Prosopistoma presence and absence?
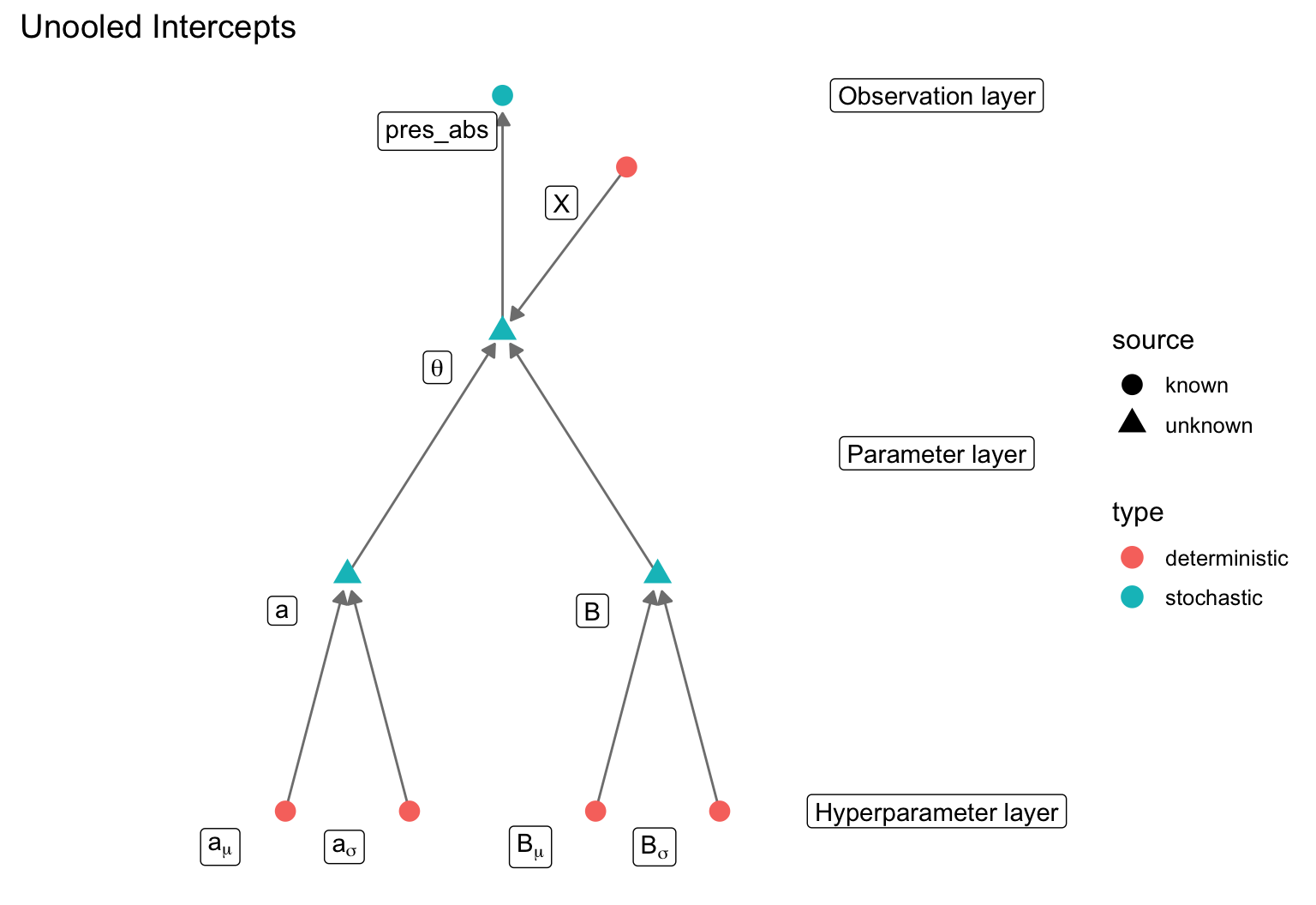
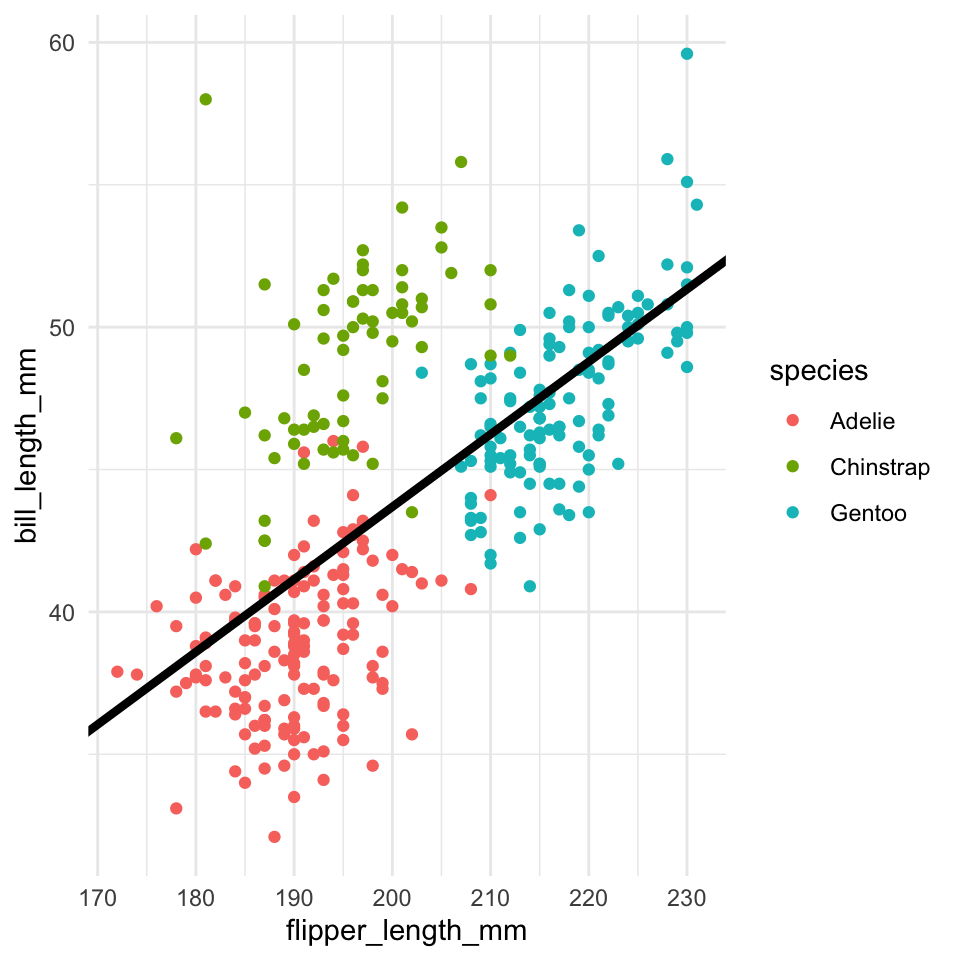
We can build an SDM using a binomial presence-absence model

data {
int <lower = 1> n; // number of data points
int <lower = 1> k; // number of variables
int <lower = 0, upper = 1> pres_abs [n];
matrix [n, k] X;
}
parameters {
real a;
vector [k] B;
}
transformed parameters {
vector <lower = 0, upper = 1> [n] theta;
prob_pres = inv_logit(a + X * B);
}
model {
pres_abs ~ binomial(1, theta);
a ~ normal(0, 10);
B ~ normal(0, 5);
}
We can imagine a two-step process:
Q1: Is the site suitable?
\[ pres\_abs \sim \mathrm{Binomial}(\theta) \]
Q2: If suitable, how many Proso are there?
\[ count \sim \mathrm{Poisson}(\lambda) \]
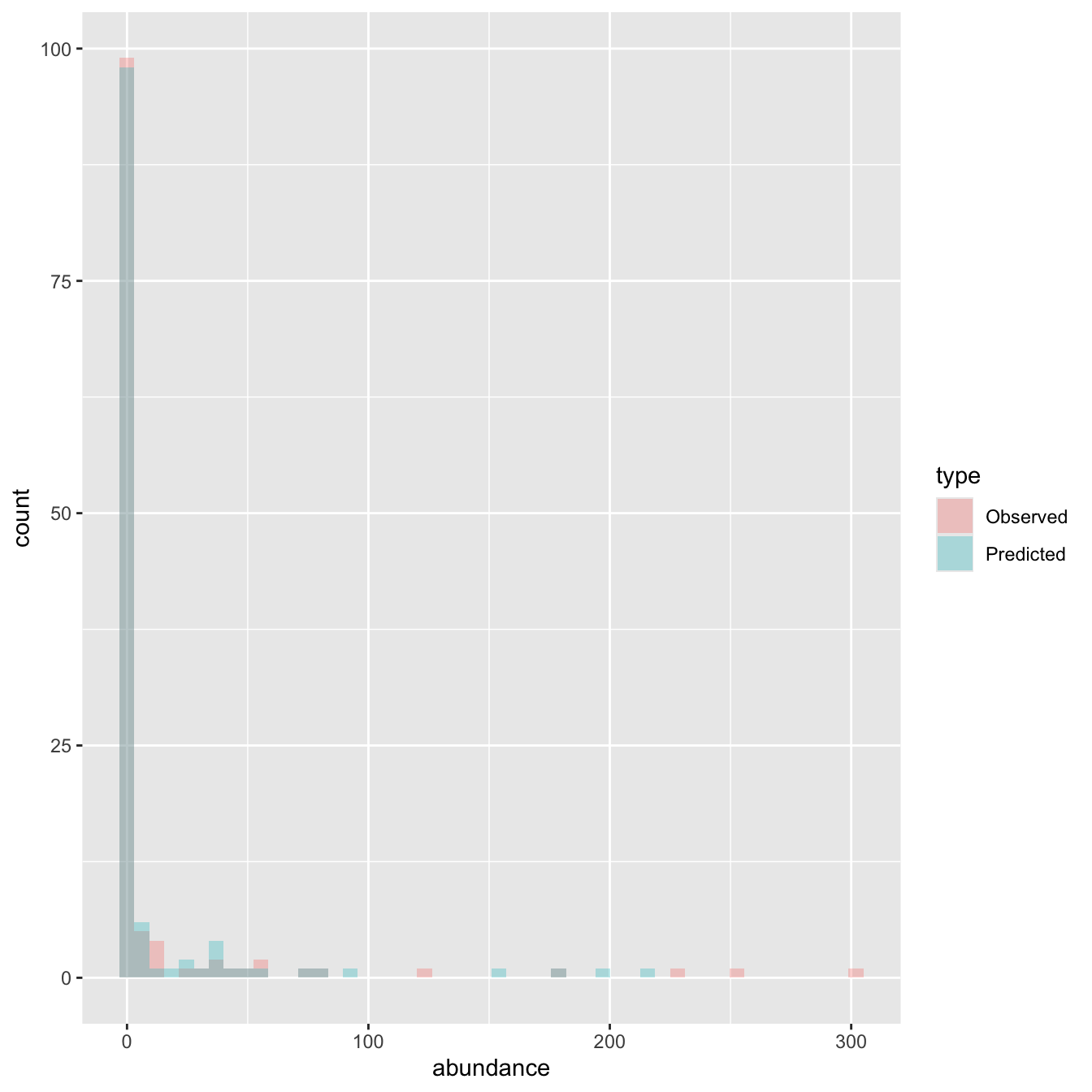
Problem: An observed count of zero can be generated in two ways! (Binomial or Poisson)
Problem: An observed count of zero can be generated in two ways! (Binomial or Poisson)
We need the addition rule and the product rule from day 1!
If \(count > 0\), we know that the species is present (with probability \(\theta\)) and it has a poisson probability, so the total probability is \(\theta \times \mathcal{P}(count | \lambda)\).
If \(count = 0\), either the site is unsuitable (with probability \(1-\theta\)) or it is suitable (prob \(\theta\)) and it has a poisson count of zero.: \((1- \theta) + \theta \times \mathcal{P}(0 | \lambda)\)
This is a zero-inflated model, a special case of a finite mixture model
\[ pr(count_i | \theta,\lambda) = \begin{cases} (1 - \theta) + \theta \times \mathcal{P}(0 | \lambda) & & count_i = 0 \\ \theta \times \mathcal{P}(count_i | \lambda) & & count_i > 0 \\ \end{cases} \]
More generally, if an observation \(y_i\) comes from a mixture of \(n\) distributions, each with parameters \(\theta_j\) and with mixing proportion \(\lambda_j\):
\[ pr(y_i | \Theta) = \sum_{j=1}^n \lambda_j \mathcal{D}(y_i | \theta_j) \]
More generally, if an observation \(y_i\) comes from a mixture of \(n\) distributions, each with parameters \(\theta_j\) and with mixing proportion \(\lambda_j\)…
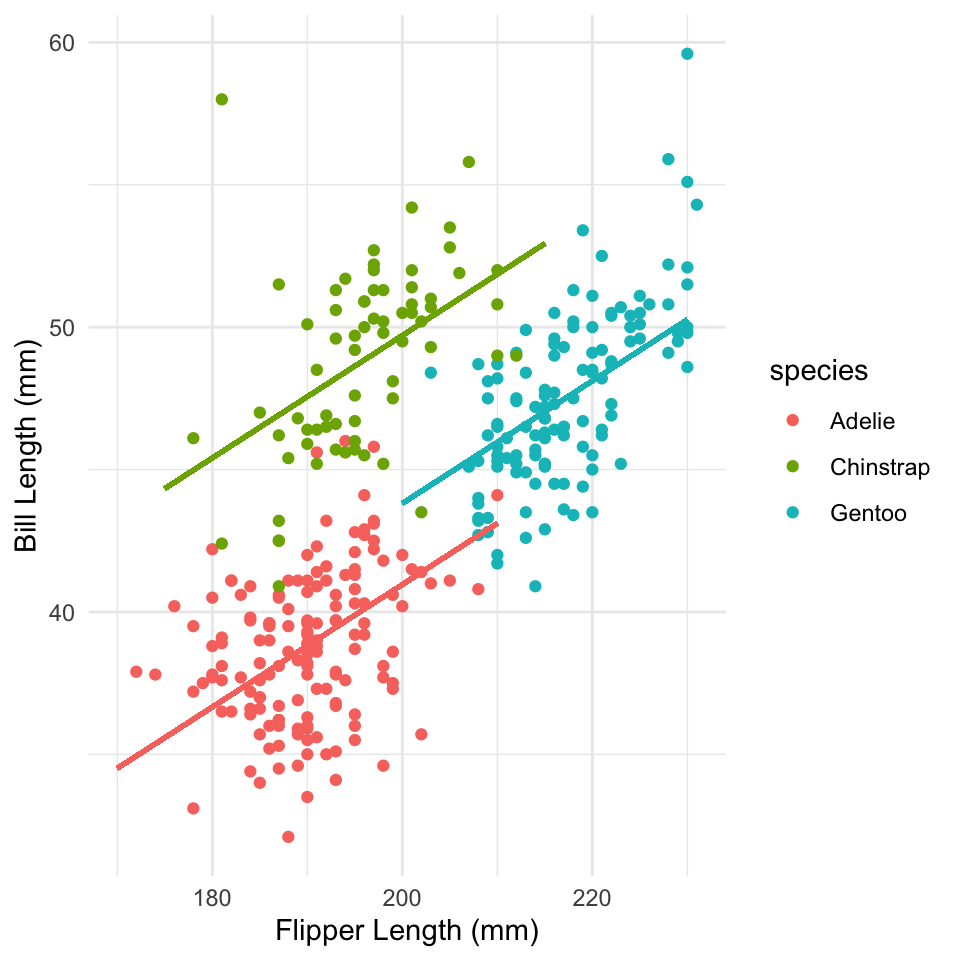
We can of course fit a regression with a link function and covariates to each distribution!
\[ \begin{aligned} pr(y_i | \Theta) & = \sum_{j=1}^n \lambda_j \mathcal{D}(y_i | \eta_{ij}, \theta_j) \\ \eta_{ij} & = \mathcal{f}_j^{-1}(a_j + \mathbf{X}_{ij}\mathbf{B}_j) \end{aligned} \]
// file: proso_mixture.stan
data {
// we split the dataset into zeros and not-zeros
// we also allow two sets of covariates, one for presence-absence and one for nonzero counts
int <lower = 0> n_zeros;
int <lower = 0> n_counts;
int <lower = 1> k_pa;
int <lower = 1> k_pois;
// four covariate matrices:
// observed zeros, presence-absence process
// observed nonzeros, presence-absence process
// observed zeros, poisson (count) process
// observed nonzeros, poisson process
matrix [n_zeros, k_pa] X_zeros_pa; // binomial process, observed zeros
matrix [n_counts, k_pa] X_count_pa; // binomial process, observed nonzeros
matrix [n_zeros, k_pois] X_zeros_pois; // poisson process, observed zeros
matrix [n_counts, k_pois] X_count_pois; // poisson process, observed zeros
// the observed nonzero counts
int <lower = 1> counts [n_counts];
// prior hyperparams
real a_pa_scale;
real B_pa_scale;
real a_pois_scale;
real B_pois_scale;
}
parameters {
// one set of linear parameters for determining the probability of presence
real a_pa;
vector [k_pa] B_pa;
// a second set of parameters for determining the count if present
real a_count;
vector [k_pois] B_count;
}
transformed parameters {
// first, we have a probability of presence and an expected count for each observed zero
vector <lower = 0, upper = 1> [n_zeros] prob_pres_zeros;
vector <lower = 0> [n_zeros] lam_zeros;
// then we have the same for each observed (nonzero) count
vector <lower = 0, upper = 1> [n_counts] prob_pres_counts;
vector <lower = 0> [n_counts] lam_counts;
prob_pres_zeros = inv_logit(a_pa + X_zeros_pa * B_pa);
lam_zeros = exp(a_count + X_zeros_pois * B_count);
prob_pres_counts = inv_logit(a_pa + X_count_pa * B_pa);
lam_counts = exp(a_count + X_count_pois * B_count);
}
model {
for(i in 1:n_zeros) {
// on the probability scale, just to see
// in the end we must work on the log scale, so it's a bit more complicated
// target *= (1 - prob_pres[i]) + prob_pres[i] * poisson_pmf(0 | lam_zeros[i]);
// log_sum_exp performs the computation above, but keeping all values on the log scale
// log_sum_exp(x1, x2) is equivalent to log(e^x1 + e^x2), but it never performs exponentiation
// x1 and x2 are kept on the log scale, so we avoid numerical problems
// see: https://mc-stan.org/docs/stan-users-guide/log-sum-of-exponentials.html
target += log_sum_exp(
// first term, the binomial term, now on the log scale
log(1 - prob_pres_zeros[i]),
// second term, the poisson term, on the log scale
log(prob_pres_zeros[i]) + poisson_lpmf(0 | lam_zeros[i])
);
}
// for the nonzero counts, we use a poisson likelihood as usual, with the added complication
// that we must account for the probability of presence!
for(i in 1:n_counts) {
target += log(prob_pres_counts[i]) + poisson_lpmf(counts[i] | lam_counts[i]);
}
a_pa ~ normal(0, a_pa_scale);
B_pa ~ normal(0, B_pa_scale);
a_count ~ normal(0, a_pois_scale);
B_count ~ normal(0, B_pois_scale);
}
generated quantities {
// capture model deviance and lppd
real deviance = 0;
vector [n_zeros + n_counts] lppd;
// simulate to get the PPD
int ppd_counts [n_zeros + n_counts];
// first simulate for all observed zeros
for(i in 1:n_zeros) {
// first term simulates the presence-absence part
// then we multiply by a simulated poisson
ppd_counts[i] = binomial_rng(1, prob_pres_zeros[i]) * poisson_rng(lam_zeros[i]);
lppd[i] = log_sum_exp(log(1 - prob_pres_zeros[i]),
log(prob_pres_zeros[i]) + poisson_lpmf(0 | lam_zeros[i]));
deviance += lppd[i];
}
// next simulate all observed nonzeros
for(j in 1:n_counts) {
ppd_counts[j + n_zeros] = binomial_rng(1, prob_pres_counts[j]) * poisson_rng(lam_counts[j]);
lppd[j + n_zeros] = log(prob_pres_counts[j]) + poisson_lpmf(counts[j] | lam_counts[j]);
deviance += lppd[j + n_zeros];
}
deviance *= -2;
}## Warning: There were 1 transitions after warmup that exceeded the maximum treedepth. Increase max_treedepth above 10. See
## https://mc-stan.org/misc/warnings.html#maximum-treedepth-exceeded
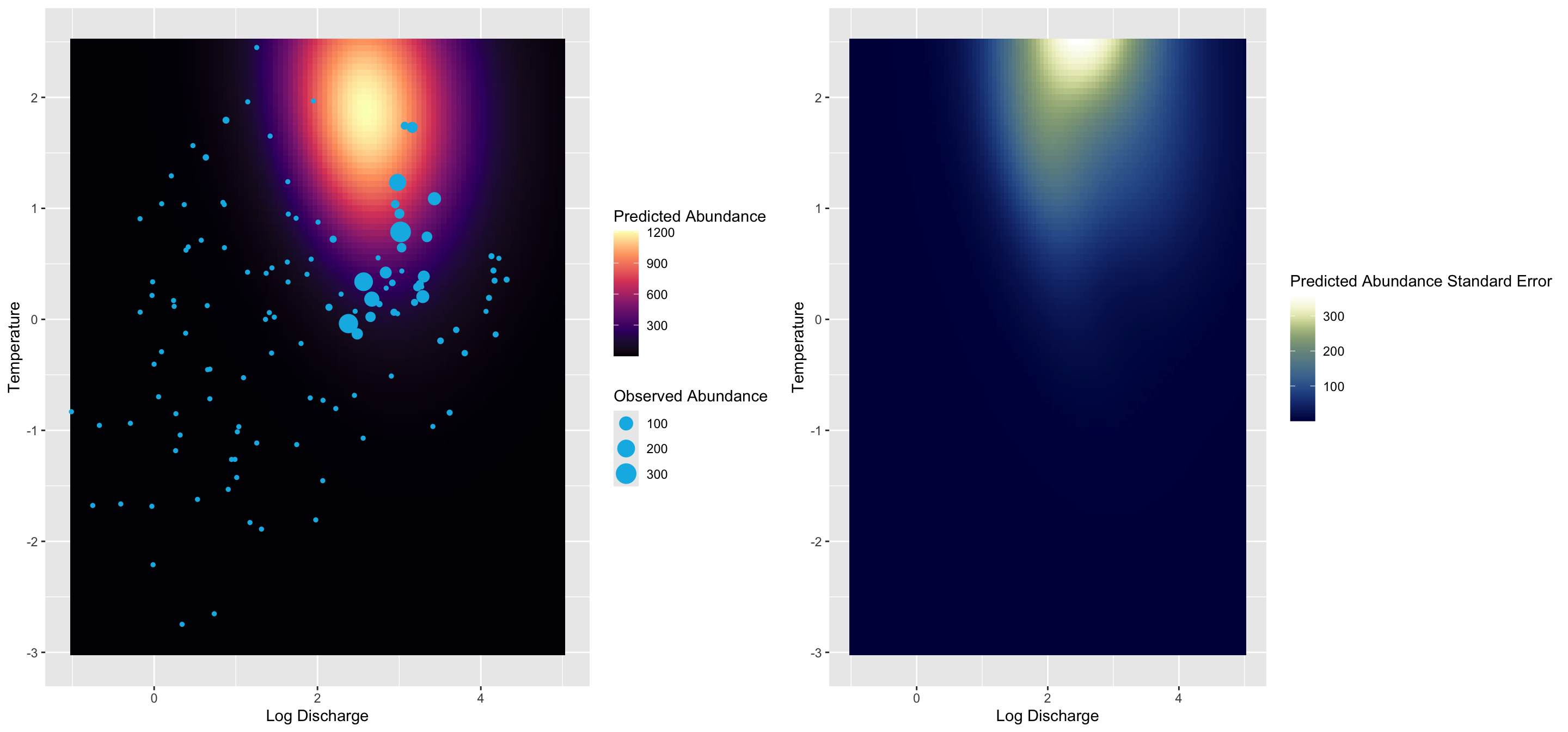
## Warning: Examine the pairs() plot to diagnose sampling problems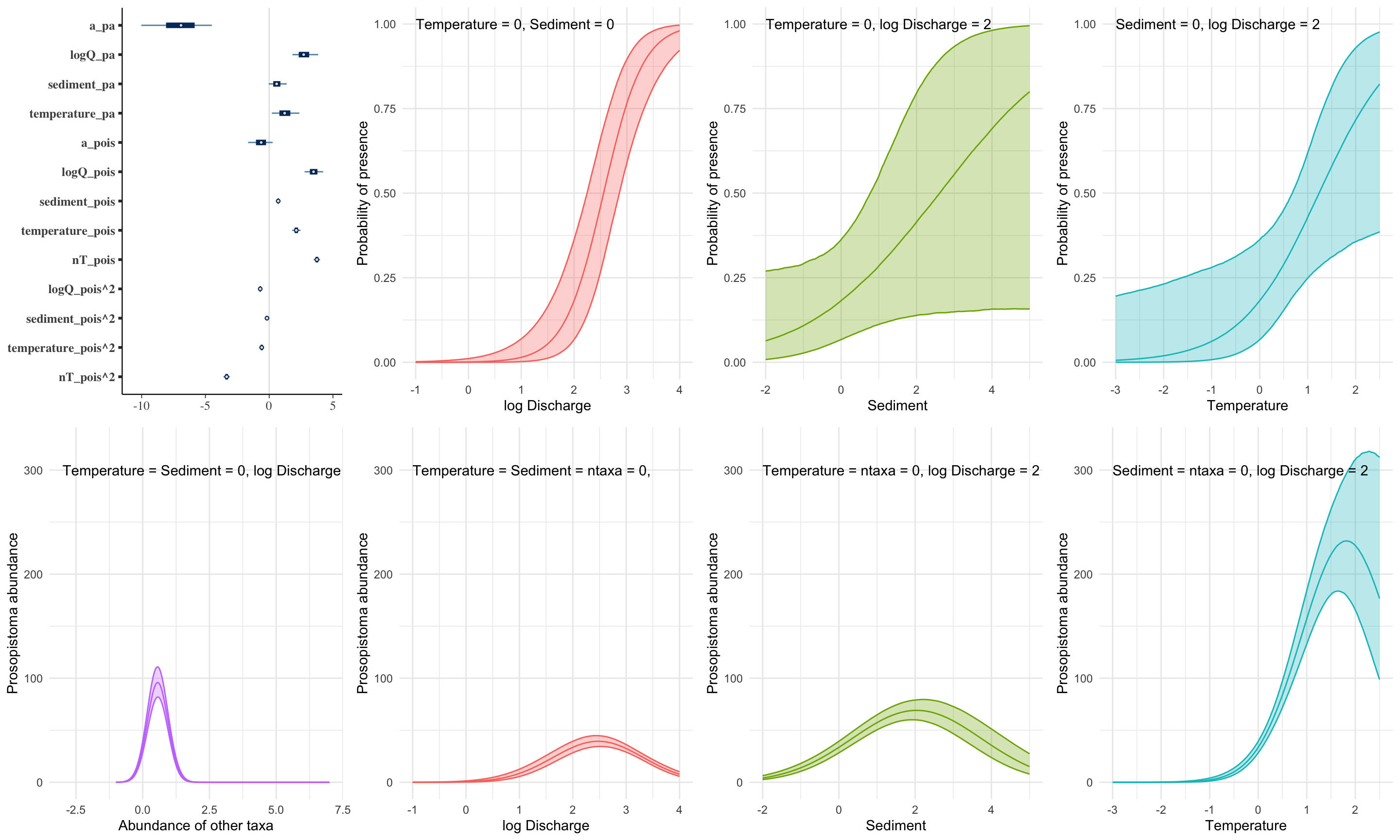
\[ \begin{aligned} \mathrm{L}[\mathbb{E}(y)] & = \alpha + \beta{\mathbf{X}} \\ \theta & = \mathcal{f}[\mathbb{E}(y)] \\ y & \sim \mathcal{D}(\theta) \\ \\ \mathrm{pr}(y_i | \color{red}{y_{-i}}, \alpha, \beta, \mathbf{X}) & \equiv \mathrm{pr}(y_i | \alpha, \beta, \mathbf{X}) \end{aligned} \]
When observation \(i\) is in group \(j\)
\[ \begin{aligned} \mathbb{E}(y_i) & = \alpha + \gamma_j + \beta X \\ y & \sim \mathcal{N}\left (\mathbb{E} \left (y \right ), \sigma \right) \\ \gamma & \sim \mathcal{N}(0, \sigma_\gamma) \end{aligned} \]
\(\gamma\) models an offset from the global intercept (hence prior mean of 0)
\[ \begin{aligned} y & \sim \mathcal{P}(\lambda E) \\ \end{aligned} \]
\[ \begin{aligned} y & \sim \mathcal{P}(\lambda E) \\ \lambda_i & = \frac{\sum_{j=1}^{\nu_i} \lambda_j}{\nu_i} \\ \end{aligned} \]
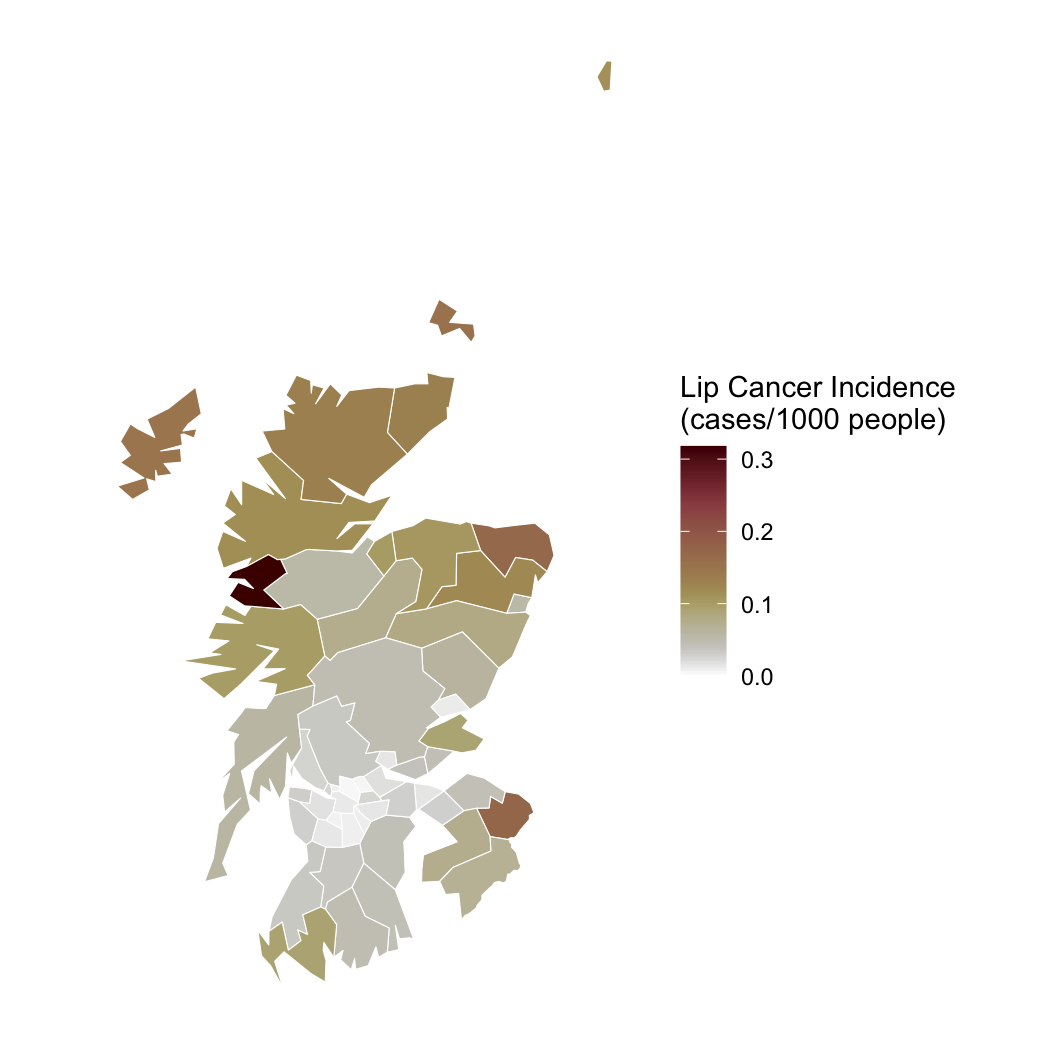
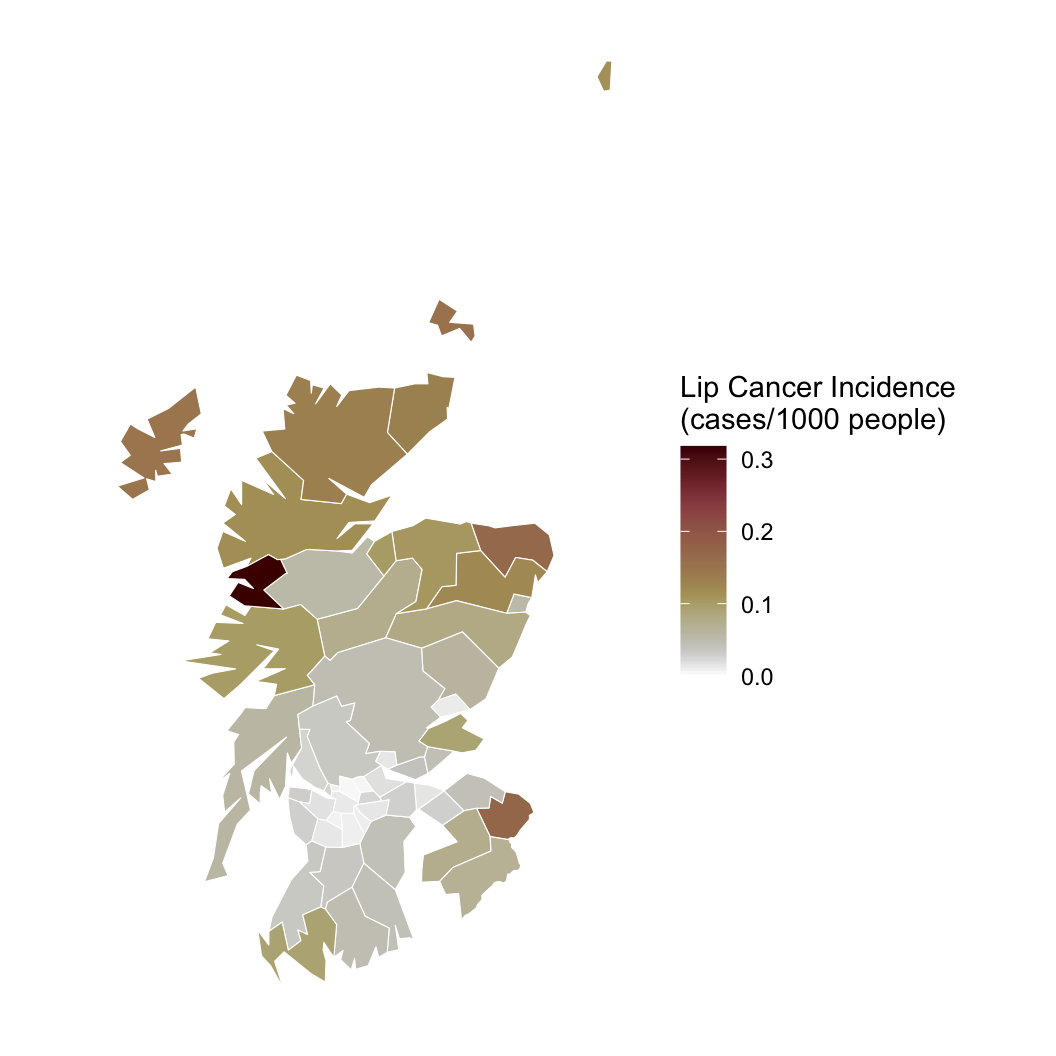
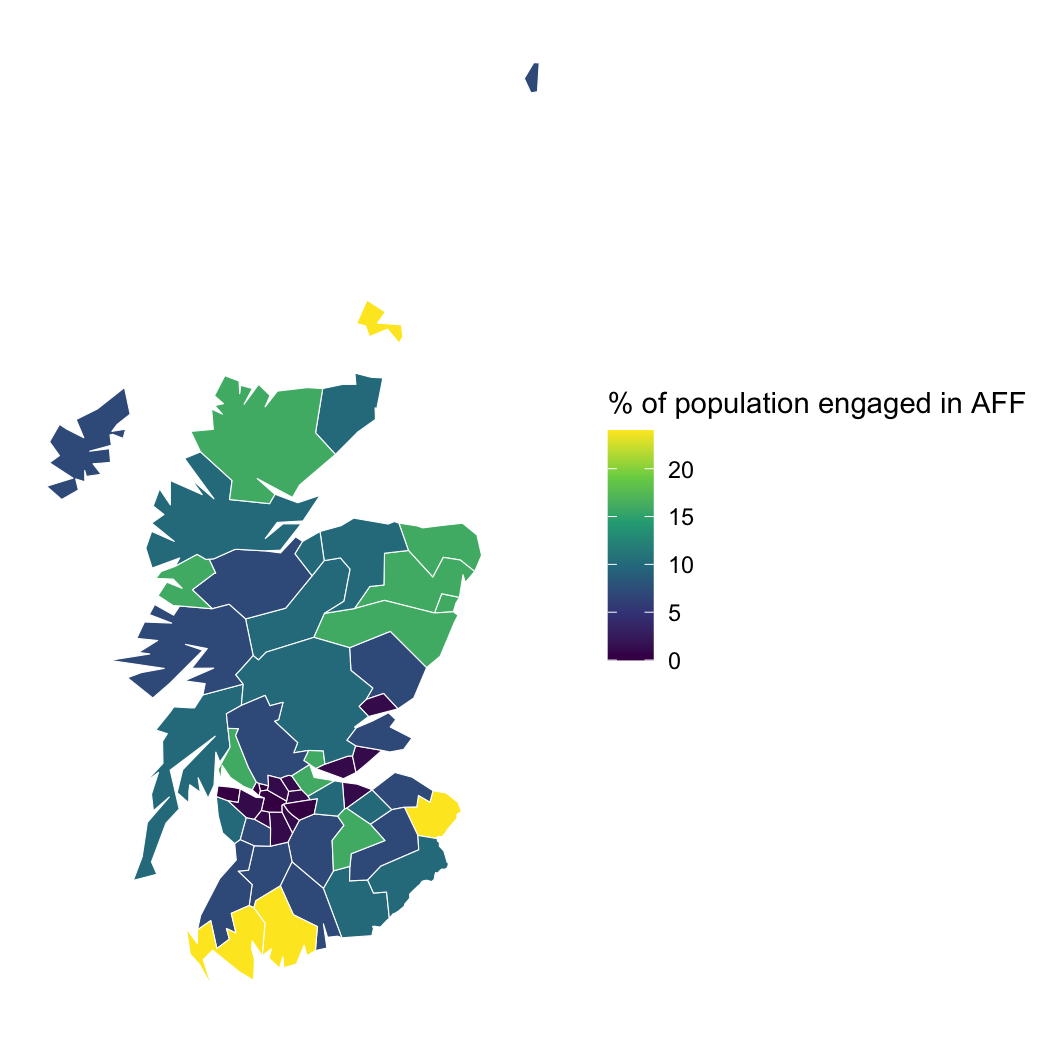
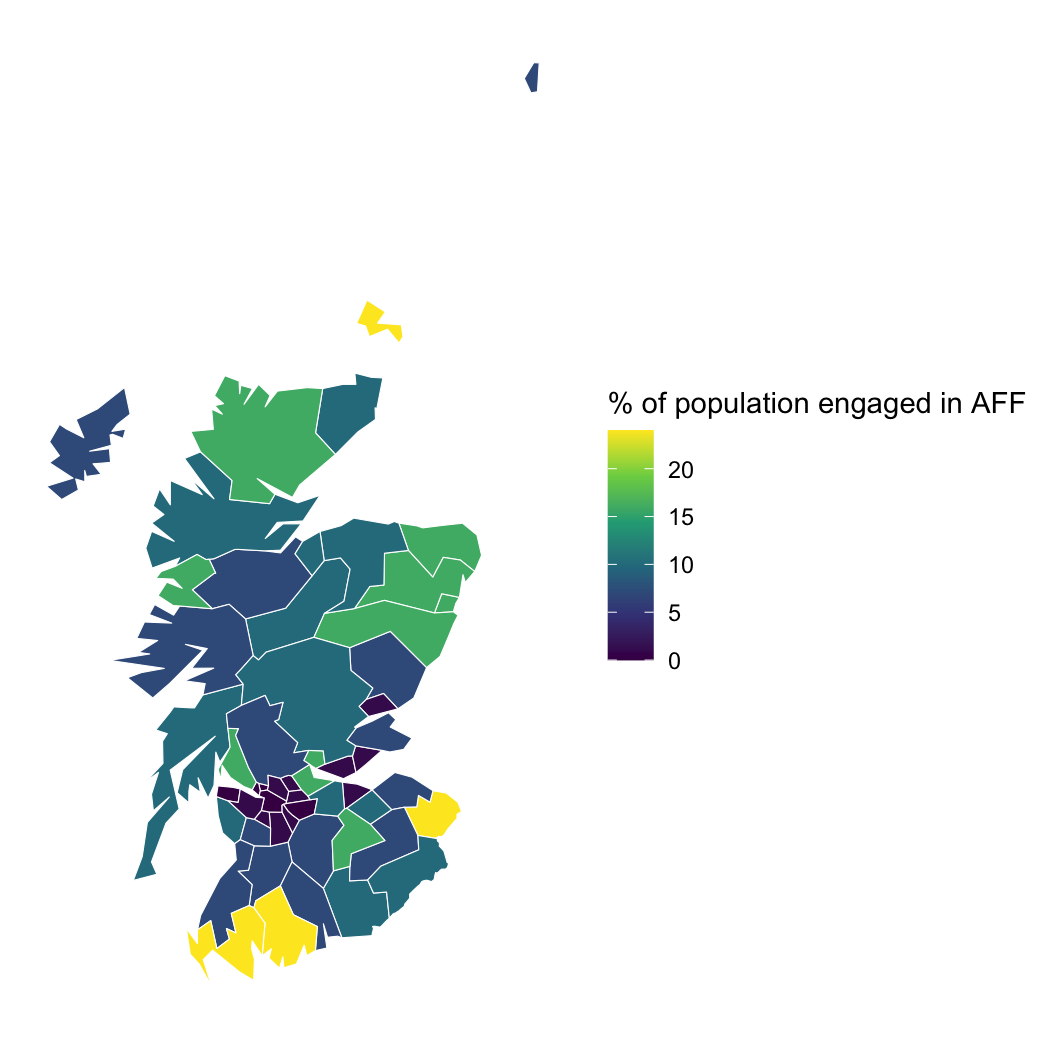
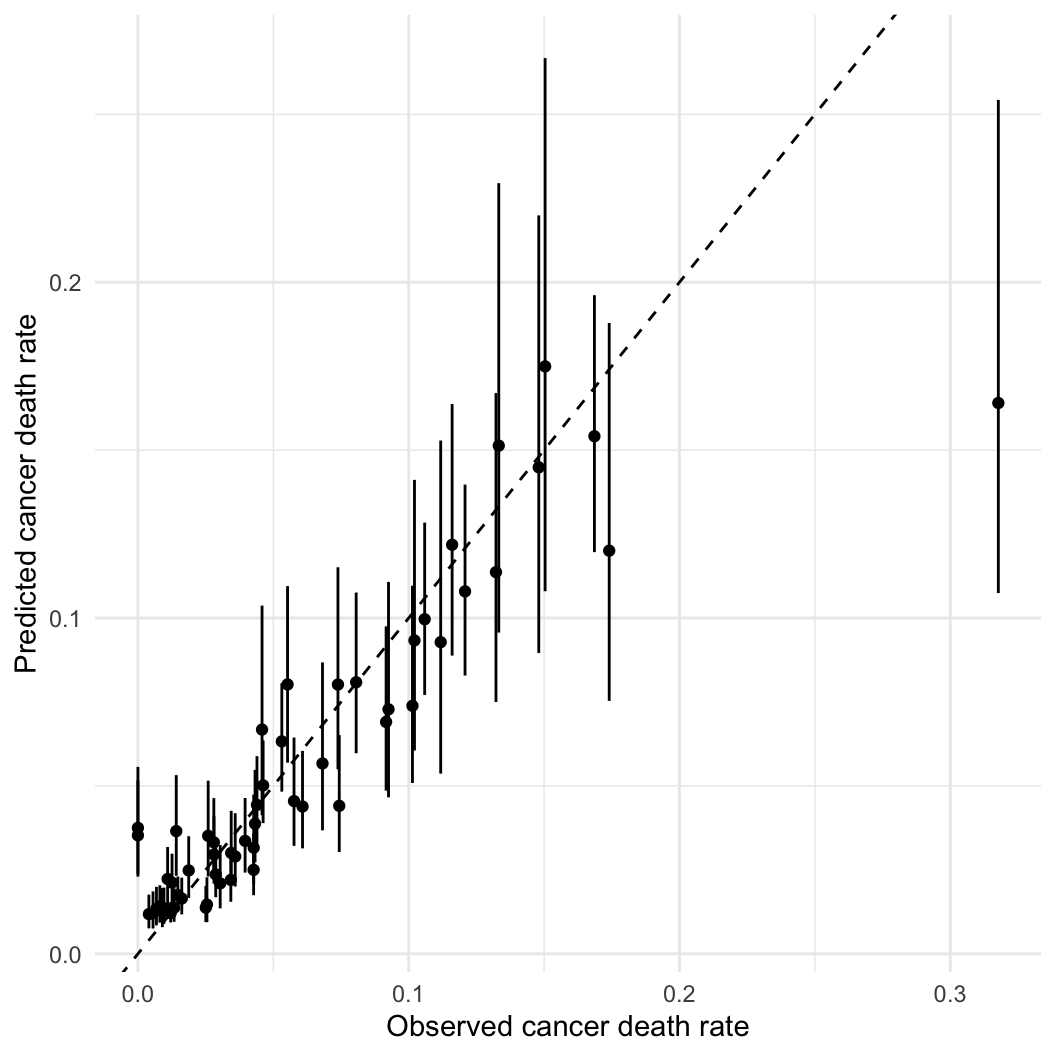
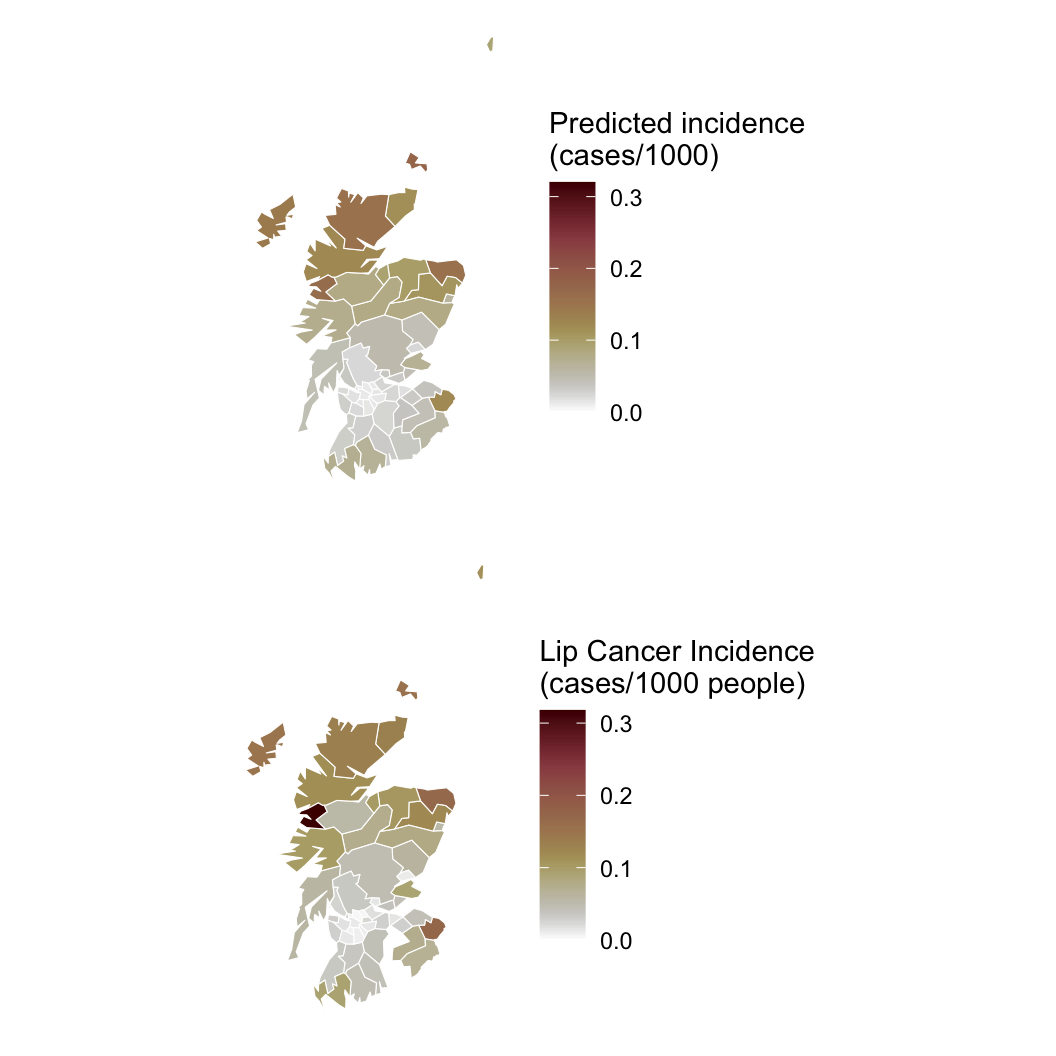
Hypothesis: Working outdoors (AFF: agriculture, forestry, and fishing) leads to lip cancer.
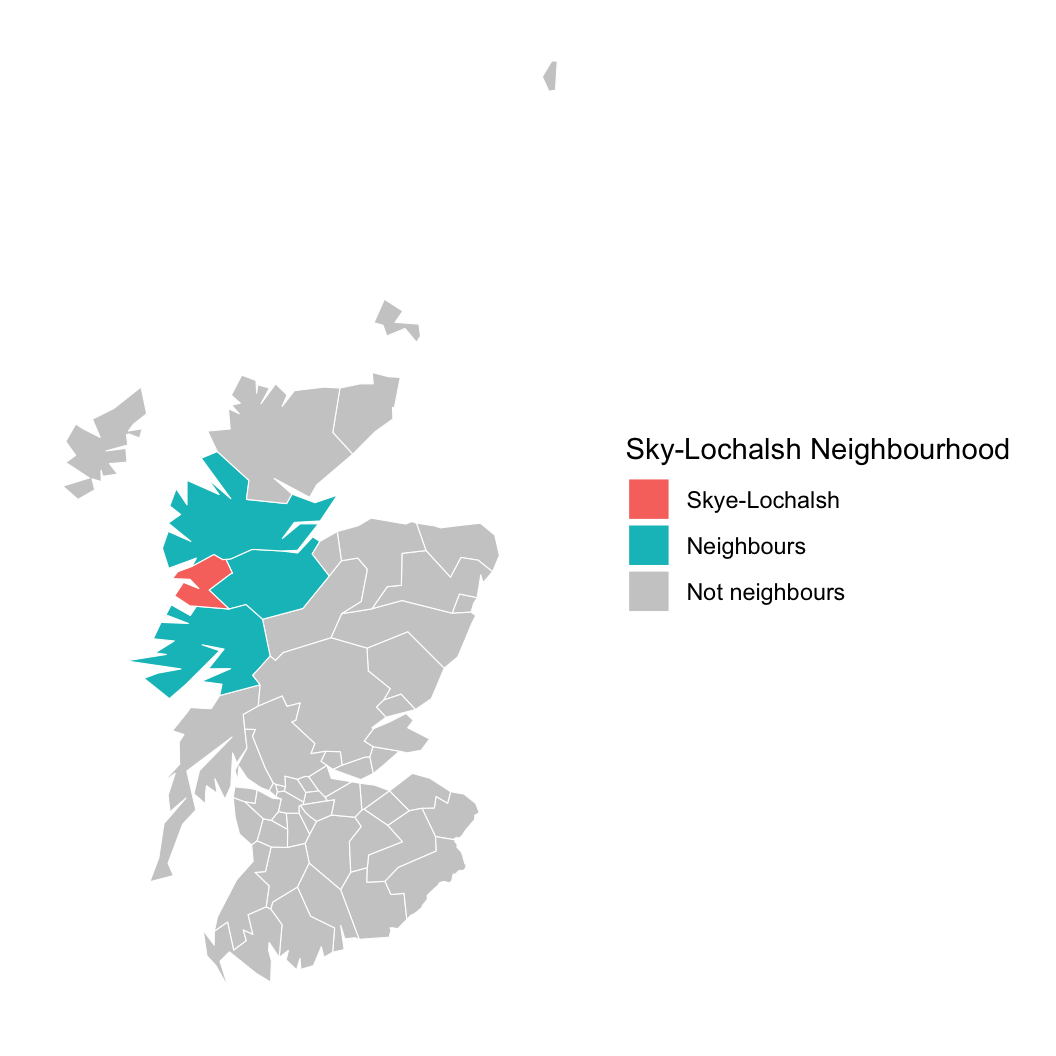
We need to account for space, or we might be wrong about AFF!
\[ \begin{aligned} y & \sim \mathcal{P}(\lambda E) \\ \lambda_i & = \frac{\sum_{j=1}^{\nu_i} \lambda_j}{\nu_i} \\ \end{aligned} \]
\[ \begin{aligned} y & \sim \mathcal{P}(\lambda E) \\ \log \lambda_i & = a + \mathbf{X}\mathbf{B} + \gamma \\ \gamma & \sim \mathcal{N}(\mu_\gamma, \sigma_\gamma) \\ \mu_{\gamma,i} & = \frac{\sum_{j=1}^nw_{i,j}\gamma_j}{\nu_i} \end{aligned} \]
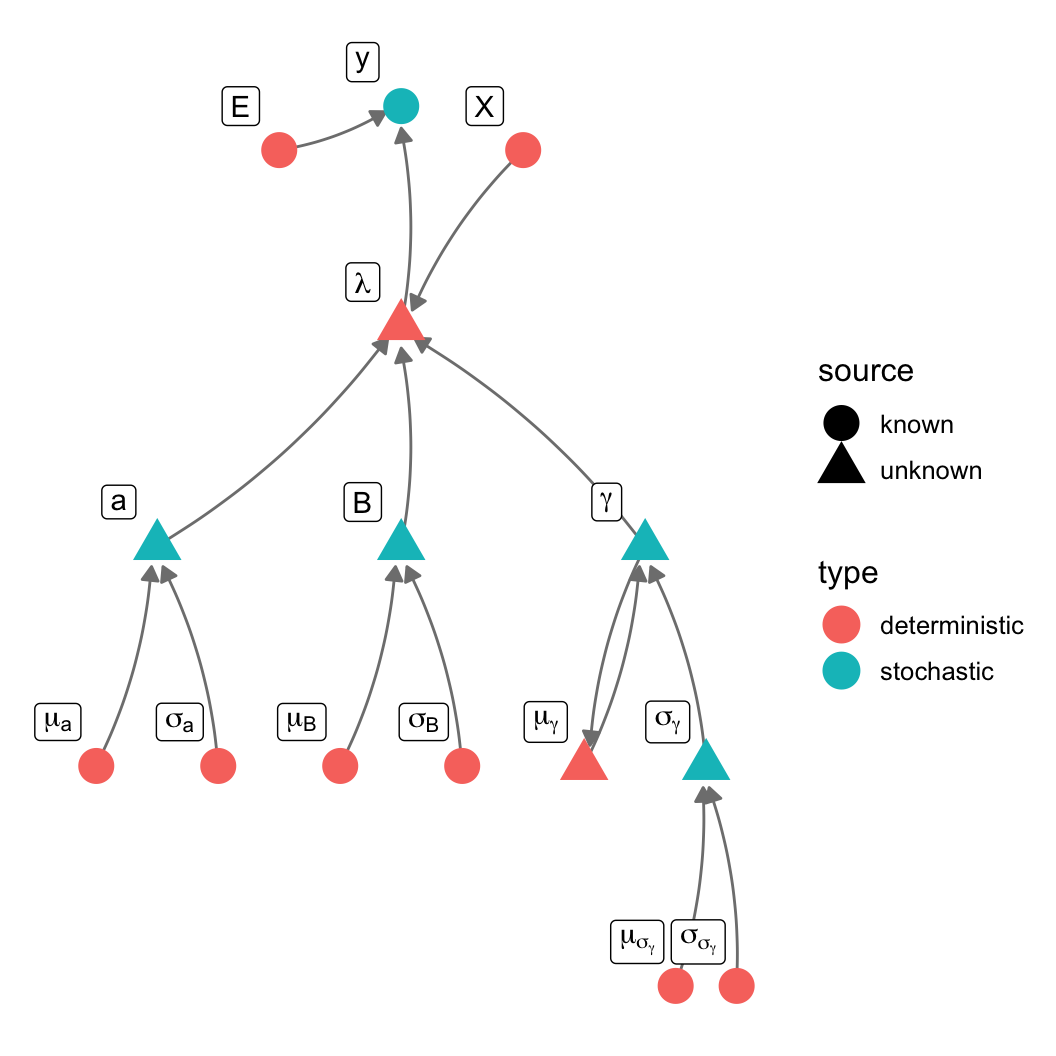
data {
int <lower = 1> n; // total number of districts, one data point per district
int <lower = 1> k; // number of regression variables
// spatial neighbourhood data
// this is a sparse array
// the district ID in column one is adjacent to column 2
int <lower = 1> n_nb; // number of adjacencies
int <lower = 1, upper = n> neighbours [n_nb, 2];
// regression data
int <lower = 0> deaths [n];
vector <lower = 0> [n] exposure;
matrix [n,k] X;
// prior hyperparams
real <lower=0> a_sig;
real <lower=0> B_sig;
// controls the strength of the spatial effect
real <lower = 0> gamma_scale_sig;
}
transformed data {
vector [n] nu = rep_vector(0, n); // number of neighbors per region
for(i in 1:n_nb)
nu[neighbours[i,1]] += 1;
}
parameters {
// regression params
real a;
vector [k] B;
// latent variable for spatial random effect
real gamma_scale;
vector [n] gamma;
}
transformed parameters {
vector [n] gamma_expectation = rep_vector(0, n);
vector <lower = 0> [n] lambda;
for(i in 1:n_nb)
gamma_expectation[neighbours[i,1]] += gamma[neighbours[i,2]];
for(i in 1:n) {
if(nu[i] > 0)
gamma_expectation[i] = gamma_expectation[i] / nu[i];
}
lambda = exp(a + gamma + X*B);
}
model {
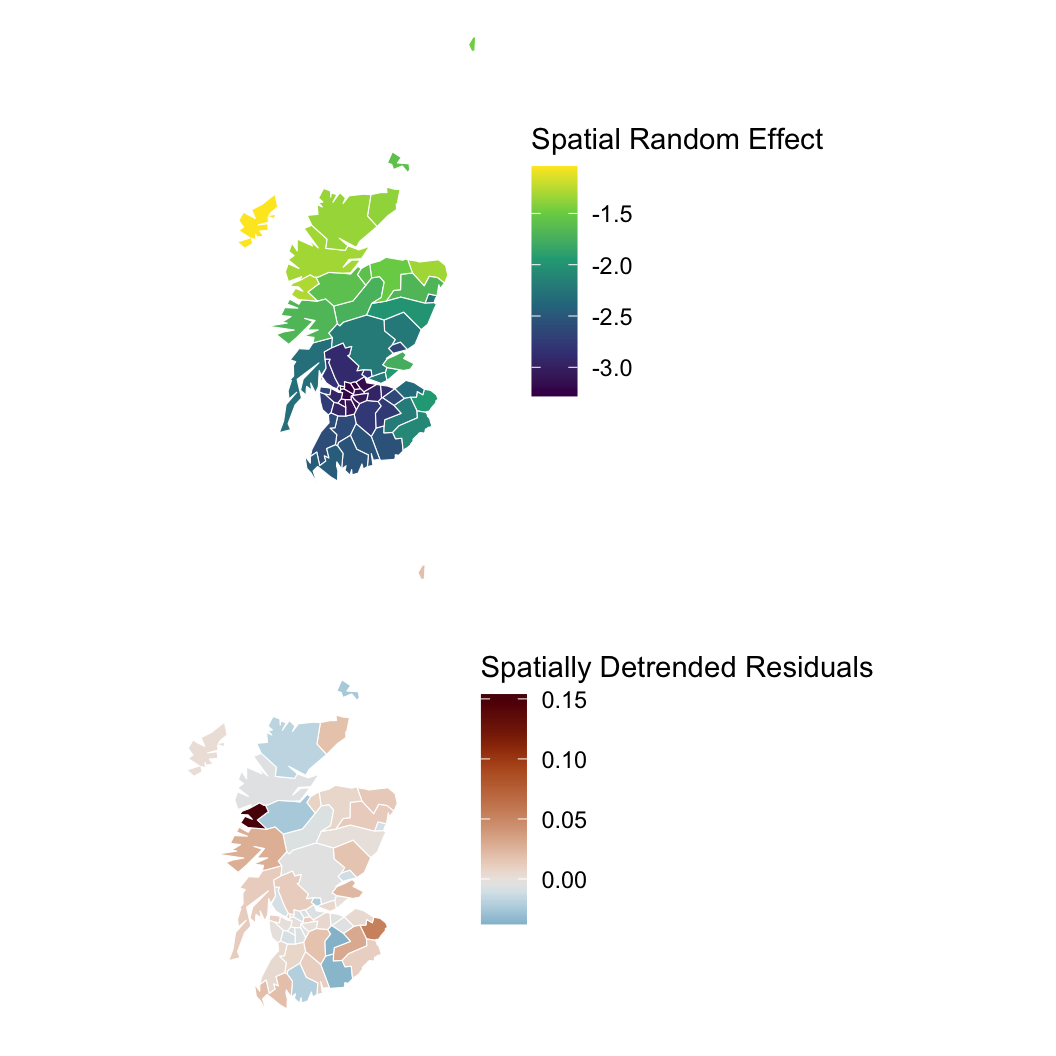
deaths ~ poisson(exposure .* lambda);
gamma ~ normal(gamma_expectation, gamma_scale);
gamma_scale ~ normal(0, gamma_scale_sig);
a ~ normal(0, a_sig);
B ~ normal(0, B_sig);
}
generated quantities {
int ppd [n];
ppd = poisson_rng(exposure .* lambda);
}library(sf)
library(rstan)
scotlip = st_read("../vu_advstats_students/data/scotlip.gpkg")
scotlip_nb = readRDS("../vu_advstats_students/data/scotlip_neighbours.rds")
## read neighbours
stan_cancer_car = stan_model("vu_advstats_students/stan/scotlip.stan")X = matrix(scotlip$AFF, ncol = 1)
standata = list(
n = nrow(scotlip),
k = ncol(X),
n_nb = nrow(scotlip_nb),
neighbours = scotlip_nb,
deaths = scotlip$CANCER,
exposure = scotlip$POP/1000,
X = X,
a_sig = 10,
B_sig = 5,
gamma_scale_sig = 10
)
# we need inits to keep the poisson function small
initfun = function() list(a = runif(1, -3,0), B = array(runif(ncol(X), -3, 0), dim = ncol(X)), gamma = runif(nrow(scotlip), -0.1, 0.1))
fit_car = sampling(cancer_car, data = standata, iter = 50000, chains = 4, control = list(max_treedepth = 20),
init = initfun, refresh = 0, open_progress = FALSE)
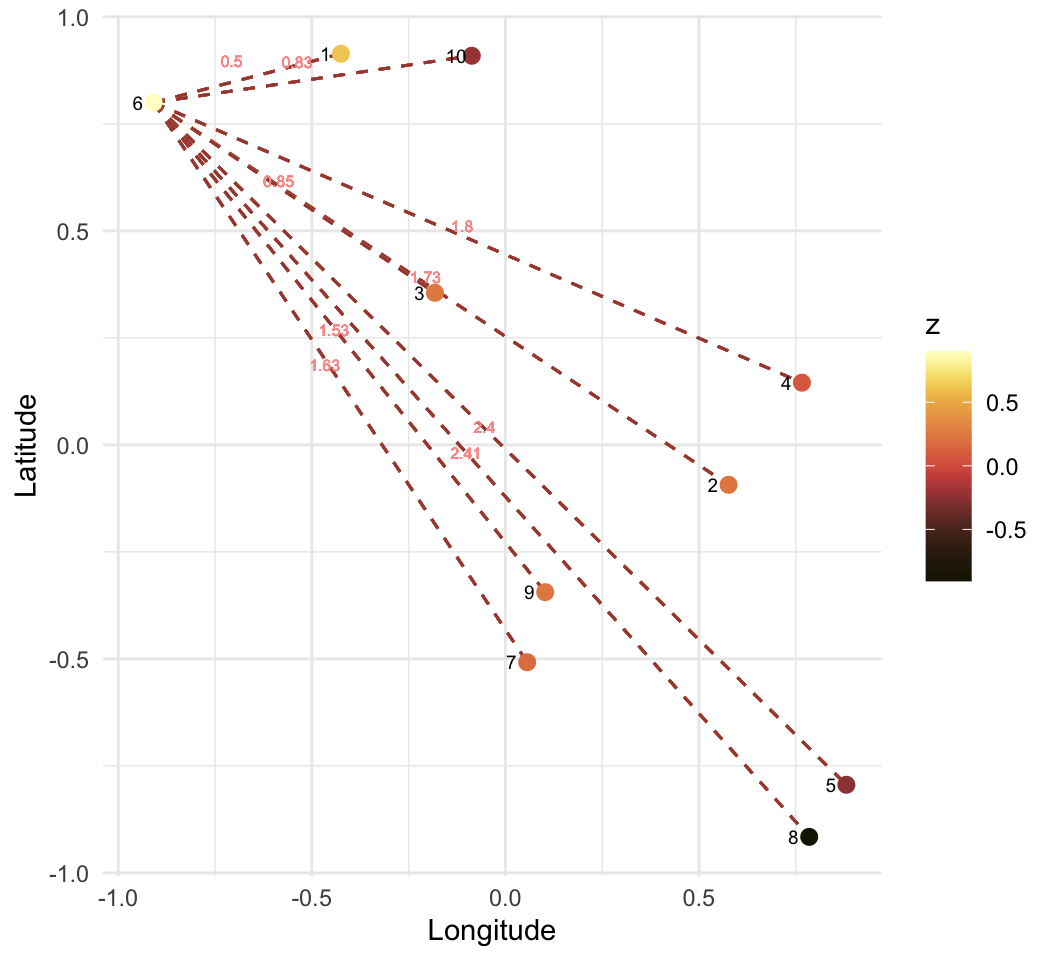
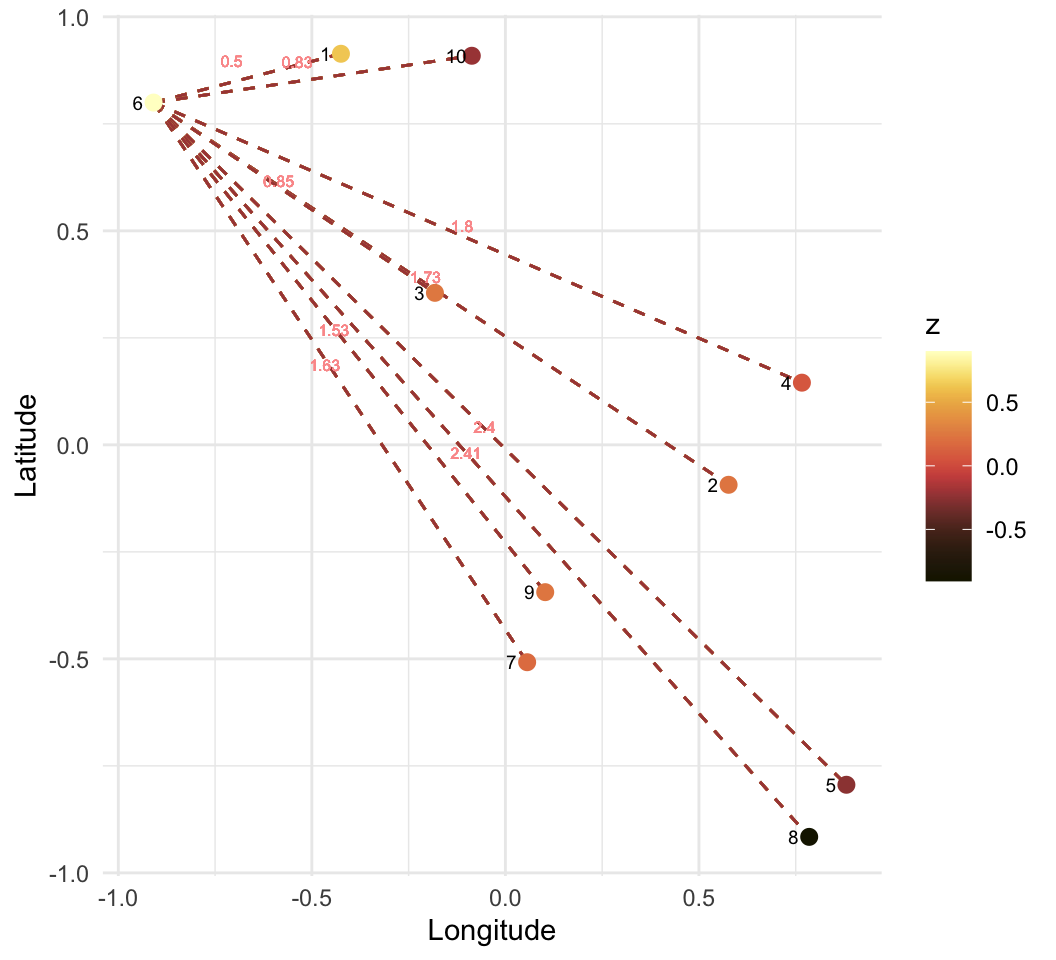
\[ w = \begin{pmatrix} Inf & 0.58 & 0.48 & 0.30 & 0.22 & 0.20 & 0.16 & 0.14 & 0.12 & 0.11 \\ 0.58 & Inf & 0.75 & 0.49 & 0.32 & 0.23 & 0.20 & 0.17 & 0.14 & 0.12 \\ 0.48 & 0.75 & Inf & 0.72 & 0.39 & 0.32 & 0.24 & 0.19 & 0.17 & 0.14 \\ 0.30 & 0.49 & 0.72 & Inf & 0.73 & 0.37 & 0.32 & 0.24 & 0.20 & 0.16 \\ 0.22 & 0.32 & 0.39 & 0.73 & Inf & 0.39 & 0.46 & 0.33 & 0.24 & 0.19 \\ 0.20 & 0.23 & 0.32 & 0.37 & 0.39 & Inf & 0.52 & 0.32 & 0.30 & 0.24 \\ 0.16 & 0.20 & 0.24 & 0.32 & 0.46 & 0.52 & Inf & 0.77 & 0.50 & 0.30 \\ 0.14 & 0.17 & 0.19 & 0.24 & 0.33 & 0.32 & 0.77 & Inf & 0.75 & 0.35 \\ 0.12 & 0.14 & 0.17 & 0.20 & 0.24 & 0.30 & 0.50 & 0.75 & Inf & 0.62 \\ 0.11 & 0.12 & 0.14 & 0.16 & 0.19 & 0.24 & 0.30 & 0.35 & 0.62 & Inf \\ \end{pmatrix} \]
\[ \begin{aligned} \mathbb{E}(y_i) & = \alpha + \gamma_{i} + \beta X \\ y & \sim \mathcal{N}\left (\mathbb{E} \left (y \right ), \sigma \right) \\ \gamma_i & \sim \mathcal{N} \left( \frac{\sum_{j=1}^{n} w_{ij} \gamma_j}{\sum_{j=1}^{n}w_{ij}}, \sigma_\gamma \right) \end{aligned} \]
Problem
\[ \begin{align} \mathbb{E}(y) & = \alpha + \beta \mathbf{X} \\ y & \sim \mathcal{MN} \left( \mathbb{E}(y), \Sigma \right) \\ \Sigma_{ij} & = \frac{\rho_{ij}}{d_{ij}} \end{align} \]
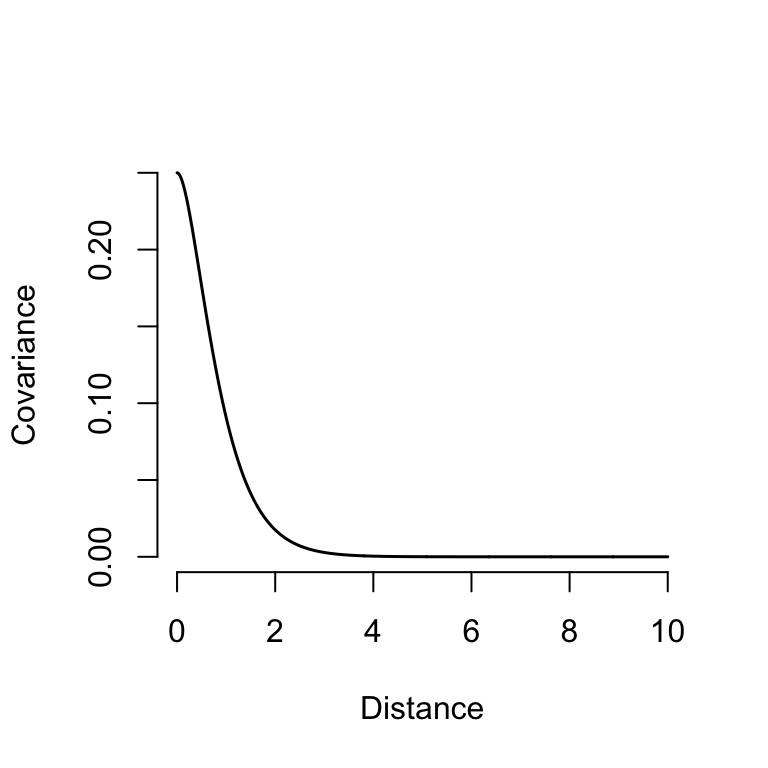
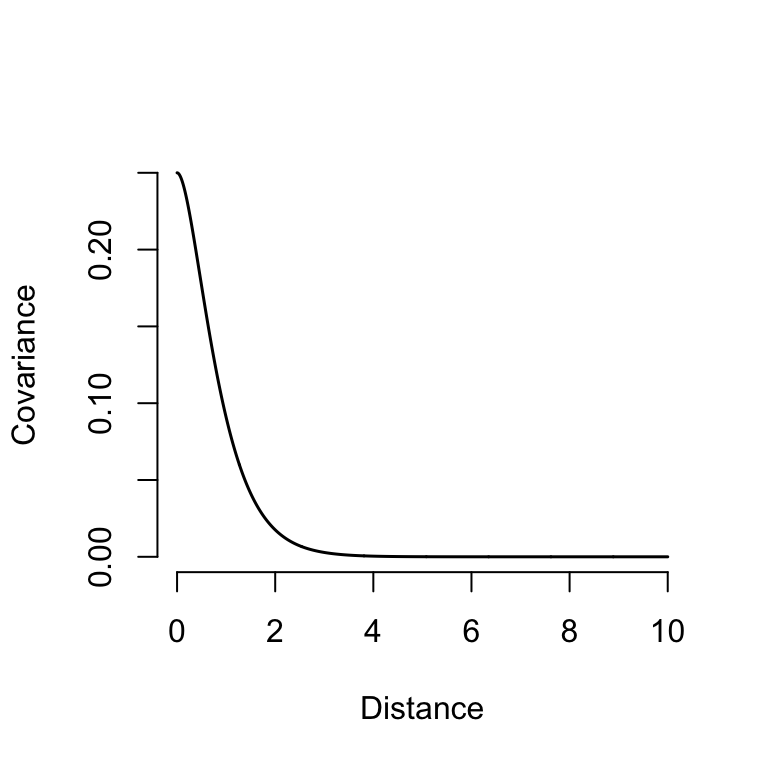
We usually use kernel functions to describe the shape of the covariance-distance relationship
A common kernel for spatial models is the Matérn\(^{3/2}\) function:
\(\sigma\): standard deviation
\(\rho\): lengthscale or correlation length
\[ \Sigma_{ij} = \sigma^2 \left( 1 + \frac{\sqrt{3}d_{ij}}{\rho}\right)\left(\mathrm{e}^\frac{-\sqrt{3}d_{ij}}{\rho} \right) \]
\[ \begin{align} \mathrm{L}[\mathbb{E}(y)] & = \alpha + \beta \mathbf{X} + \gamma \\ \theta &= \mathcal{f}[\mathbb{E}(y), \phi] \\ y & \sim \mathcal{D}(\theta) \\ \gamma & \sim \mathcal{MN} \left( \mathbf{0}, \Sigma \right) \\ \Sigma_{ij} & = \sigma^2 \left( 1 + \frac{\sqrt{3}d_{ij}}{\rho}\right)\left(\mathrm{e}^\frac{-\sqrt{3}d_{ij}}{\rho} \right) \end{align} \]
## Ignoring unknown labels:
## • fill : "y"